Тема 1. Основы финансовых вычислений

ФИНАНСЫ

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

К ПРАКТИЧЕСКИМ ЗАНЯТИЯМ

И САМОСТОЯТЕЛЬНОЙ РАБОТЕ

для студентов специальности 080109 «Бухгалтерский учет, анализ и аудит»

всех форм обучения

ТЮМЕНЬ, 2013

ББК: У9(2)262

Сбитнев, А.Е. Финансы: методические указания к практическим занятиям и самостоятельной работе для студентов специальности 080109 «Бухгалтерский учет, анализ и аудит» всех форм обучения / А.Е. Сбитнев. – Тюмень: РИО ФГБОУ ВПО «ТюмГАСУ», 2013. – 32 с.

Методические указания разработаны на основании рабочих программ дисциплины «Финансы» ФГБОУ ВПО «ТюмГАСУ» специальности 080109 «Бухгалтерский учет, анализ и аудит» всех форм обучения.

Методические указания содержат задачи с решениями по основным темам практических занятий, а также задания для самостоятельной работы, направленные на формирование у студентов практических навыков выполнения финансовых расчетов.

Рецензент: Васильев Е.В.

Тираж 50 экз.

© ФГБОУ ВПО «Тюменский государственный архитектурно-строительный университет»

© Сбитнев А.Е.

© Редакционно-издательский отдел ФГБОУ ВПО «Тюменский государственный архитектурно-строительный университет»

СОДЕРЖАНИЕ

ВВЕДЕНИЕ
ТЕМА 1. ОСНОВЫ ФИНАНСОВЫХ ВЫЧИСЛЕНИЙ
ТЕМА 2. ОЦЕНКА ФИНАНСОВОГО СОСТОЯНИЯ ОРГАНИЗАЦИИ
ТЕМА 3. АНАЛИЗ РИСКОВ ОРГАНИЗАЦИИ
ТЕМА 4. РАСЧЕТ СХЕМ ПОГАШЕНИЯ КРЕДИТА
БИБЛИОГРАФИЧЕСКИЙ СПИСОК

ВВЕДЕНИЕ

Методические указания к практическим занятиям и самостоятельной работе для студентов специальности 080109 «Бухгалтерский учет, анализ и аудит» всех форм обучения составлены в соответствии с ГОС ВПО ОПД.Ф.07 «Финансы» и раскрывают следующие разделы дисциплины: финансовое планирование и прогнозирование; основы функционирования финансов коммерческих предприятий.

Целью данных методических указаний является закрепление знаний, полученных в ходе теоретическо­го изучения дисциплины «Финансы» и навыков решения практических задач.

Задачи с решениями знакомят студентов с различными приемами выполнения финансовых расчетов. Задачи для самостоятельной работы развивают навыки индивидуальной работы на ос­нове приемов и методов, представленных в задачах с решениями.

Решение достаточно большого количества задач в ходе проведения практических занятий позволит студентам:

- находитьконкретные подходы, схемы и модели решения финансовых задач;

- проводить финансовый анализ и оценивать финансовое состояние организаций;

- выбирать оптимальные финансовые решения, используя современные подходы, методы и финансовые инструменты.

ТЕМА 1. ОСНОВЫ ФИНАНСОВЫХ ВЫЧИСЛЕНИЙ

В данной теме рассматриваются операции с процентными ставками и прикладные аспекты финансовых рент.

Наращение капитала с использованием схемы простых процентов осуществляется по формуле (1):

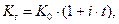(1)

где 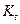– накопленная величина капитала за период времени t;

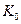– первоначальная величина капитала в момент времени t=0;

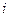– процентная ставка (ставка доходности).

Наращение капитала с использованием схемы сложных процентов осуществляется по формуле (2):

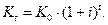(2)

Для дисконтирования с использованием схем простых и сложных процентов применяются формулы (3)-(4):

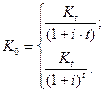		(3)
(4)

Расчет времени наращения капитала с использованием схем простых и сложных процентов осуществляется на основе формул (5)-(6):

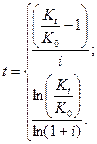		(5)
(6)

Величина процентной ставки определяется по формулам (7)-(8):

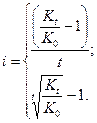		(7)
(8)

Расчет реальной процентной ставки осуществляется с использованием формулы И. Фишера:

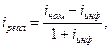(9)

где 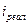– значение реальной процентной ставки;

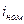– значение номинальной процентной ставки;

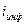– уровень инфляции.

Финансовые ренты представляют собой потоки платежей, осуществляемых через равные промежутки времени.

Выделяют накопленную (компаундированную) и современную (дисконтированную, приведенную) величину ренты.

Формулы расчета накопленной и современной величины ренты зависят от конкретной ситуации.

Ситуация 1. Величина ренты не постоянна во времени (варьирует); процентная ставка остается неизменной на протяжении всего расчетного периода:

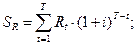		(10)
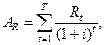		(11)

где 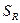– накопленная величина ренты;

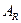– современная величина ренты;

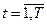– номера периодов времени;

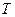– продолжительность расчетного периода;

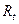– величина ренты в периоде времени t.

Ситуация 2. Величина ренты и процентной ставки не постоянны во времени:

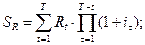		(12)
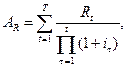		(13)

где 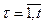– номера периодов времени;

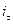– размер процентной ставки в периоде времени .

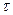Ситуация 3. Величина ренты и процентной ставки неизменны на протяжении всего расчетного периода:

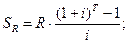		(14)
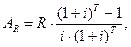		(15)

где 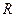– размер постоянной ренты.

Примеры решения задач:

Задача 1.

На депозитном счете было размещено 20000 руб. Депозитная процентная ставка составляет 7% годовых. Определить, какая сумма будет на счете через 4 года, если используется:

а) схема простых процентов;

б) схема сложных процентов.

Решение:

При использовании схемы простых процентов накопленная величина капитала составит (формула (1)):

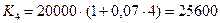руб.

При использовании схемы сложных процентов накопленная величина капитала составит (формула (2)):

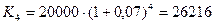руб.

Ответ:

Через 4 года на депозитном счете будет находиться сумма в размере:

а) 25600 руб., если используется схема простых процентов;

б) 26216 руб., если используется схема сложных процентов.

Задача 2.

Депозитная процентная ставка составляет 8% годовых. Определить, какую сумму необходимо разместить в банке, чтобы через 6 лет размер средств на депозитном счете составил 340000 руб., если используется:

а) схема простых процентов;

б) схема сложных процентов.

Решение:

При использовании схемы простых процентов первоначальная величина капитала составит (формула (3)):

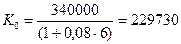руб.

При использовании схемы сложных процентов первоначальная величина капитала составит (формула (4)):

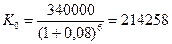руб.

Ответ:

Для того чтобы через 6 лет размер средств на депозитном счете составил 340000 руб. в банке необходимо разместить:

а) 229730 руб., если используется схема простых процентов;

б) 214258 руб., если используется схема сложных процентов.

Задача 3.

Размер депозитного вклада составляет 90000 руб., депозитная процентная ставка – 7,5% годовых. Определить, за какой период времени размер средств на депозитном счете составит 120000 руб., если используется:

а) схема простых процентов;

б) схема сложных процентов.

Решение:

При использовании схемы простых процентов время наращения капитала составит (формула (5)):

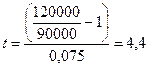года.

При использовании схемы сложных процентов время наращения капитала составит (формула (6)):

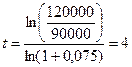года.

Ответ:

Период времени, необходимый для того, чтобы размер средств на депозитном счете оказался равным 120000 руб., составляет:

а) 4,4 года, если используется схема простых процентов;

б) 4 года, если используется схема сложных процентов.

Задача 4.

На депозитном счете было размещено 480000 руб. сроком на 5 лет. В конце расчетного периода общая сумма средств составила 690000 руб. Определить годовой размер депозитной процентной ставки, если используется:

а) схема простых процентов;

б) схема сложных процентов.

Решение:

При использовании схемы простых процентов годовой размер депозитной процентной ставки составит (формула (7)):

.

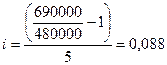При использовании схемы сложных процентов годовой размер депозитной процентной ставки составит (формула (8)):

.

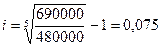Ответ:

Годовой размер депозитной процентной ставки составляет:

а) 8,8%, если используется схема простых процентов;

б) 7,5%, если используется схема сложных процентов.

Задача 5.

Депозитная процентная ставка составляет 8,5% годовых; прогнозируемый уровень инфляции в годовом исчислении – 6,2%. Определить реальную годовую доходность размещения средств на депозитном счете.

Решение:

Реальная годовая доходность размещения средств на депозитном счете определяется с использованием формулы (9):

.

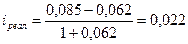Ответ:

Реальная годовая доходность депозитного вклада составляет 2,2%.

Задача 6.

Определить накопленную и современную величину финансовой ренты на основе данных, представленных в таблице 1, при условии, что процентная ставка составляет 10% годовых.

Таблица 1 – Потоки платежей на конец соответствующего года

Год
Размер платежа, тыс. руб.

Решение:

Расчет накопленной и современной величины ренты осуществляется исходя из условий, соответствующих ситуации 1, по формулам (10)-(11):

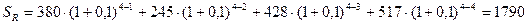тыс. руб.;

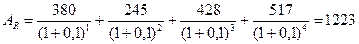тыс. руб.

Ответ:

Накопленная величина финансовой ренты составляет 1790 тыс. руб., современная величина платежей – 1223 тыс. руб.

Задача 7.

Определить накопленную и современную величину финансовой ренты на основе данных, представленных в таблице 2.

Таблица 2 – Потоки платежей на конец соответствующего года

и процентные ставки

Год
Размер платежа, тыс. руб.
Размер процентной ставки, %

Решение:

Расчет накопленной и современной величины ренты осуществляется исходя из условий, соответствующих ситуации 2, по формулам (12)-(13):

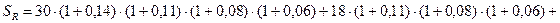
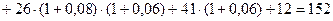тыс. руб.;

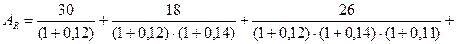
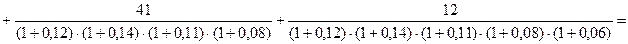93 тыс. руб.

Ответ:

Накопленная величина финансовой ренты составляет 152 тыс. руб., современная величина платежей – 93 тыс. руб.

Задача 8.

На депозитном счете в банке ежегодно размещались средства в размере 50000 руб. Депозитная процентная ставка составляет 7% годовых. Определить, какая сумма будет на счете через 8 лет.

Решение:

Накопленная величина средств на депозитном счете определяется по формуле (14):

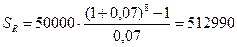руб.

Ответ:

Через 8 лет размер средств на депозитном счете составит 512990 руб.

Задача 9.

Заемщик ежегодно в течение 4 лет погашает кредит в банке (включая основной долг и проценты) в размере 630478 руб. Определить размер кредита при условии, что кредитная процентная ставка составляет 15% годовых.

Решение:

Величина взятого кредита определяется по формуле (15):

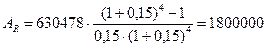руб.

Ответ:

Размер кредита составляет 1800000 руб.

Задачи для самостоятельного решения:

Задача 1.

На депозитном счете было размещено 75000 руб. Депозитная процентная ставка составляет 8% годовых. Определить, какая сумма будет на счете через 3 года, если используется:

а) схема простых процентов;

б) схема сложных процентов.

Задача 2.

Депозитная процентная ставка составляет 6,5% годовых. Определить, какую сумму необходимо разместить в банке, чтобы через 5 лет размер средств на депозитном счете составил 800000 руб., если используется:

а) схема простых процентов;

б) схема сложных процентов.

Задача 3.

Размер депозитного вклада составляет 42000 руб., депозитная процентная ставка – 7% годовых. Определить, за какой период времени размер средств на депозитном счете составит 60000 руб., если используется:

а) схема простых процентов;

б) схема сложных процентов.

Задача 4.

На депозитном счете было размещено 230000 руб. сроком на 6 лет. В конце расчетного периода общая сумма средств составила 370000 руб. Определить годовой размер депозитной процентной ставки, если используется:

а) схема простых процентов;

б) схема сложных процентов.

Задача 5.

Депозитная процентная ставка составляет 9% годовых; прогнозируемый уровень инфляции в годовом исчислении – 6,7%. Определить реальную годовую доходность размещения средств на депозитном счете.

Задача 6.

Определить накопленную и современную величину финансовой ренты на основе данных, представленных в таблице 3, при условии, что процентная ставка составляет 12% годовых.

Таблица 3 – Потоки платежей на конец соответствующего года

Год
Размер платежа, тыс. руб.

Задача 7.

Определить накопленную и современную величину финансовой ренты на основе данных, представленных в таблице 4.

Таблица 4 – Потоки платежей на конец соответствующего года

и процентные ставки

Год
Размер платежа, тыс. руб.
Размер процентной ставки, %

Задача 8.

На депозитном счете в банке ежегодно размещались средства в размере 35000 руб. Депозитная процентная ставка составляет 8% годовых. Определить, какая сумма будет на счете через 6 лет.

Задача 9.

Заемщик ежегодно в течение 3 лет погашает кредит в банке (включая основной долг и проценты) в размере 86000 руб. Определить размер кредита при условии, что кредитная процентная ставка составляет 17% годовых.