Пример. 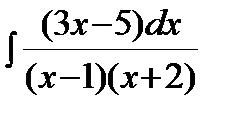 .
.
Решение. Сначала разложим дробь на простейшие:
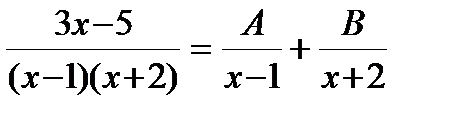 .
.
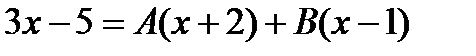 .
.
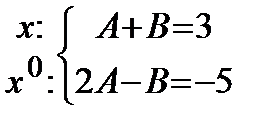 .
.
Решая систему, получим: 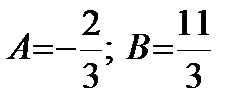 .
.
Тогда исходный интеграл примет вид:
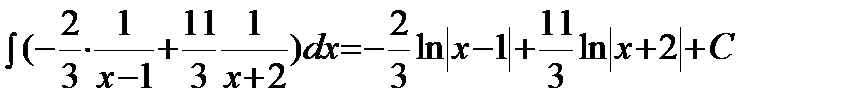 .
.
Пример. 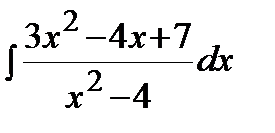 .
.
Решение. Так как дробь является неправильной, то сначала выделим целую часть. В результате получим:
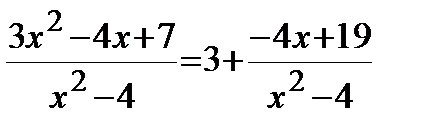 .
.
Теперь вычислим интеграл:
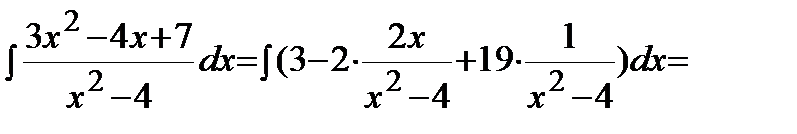
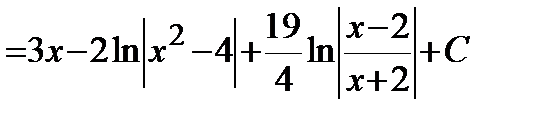 .
.
Пример. 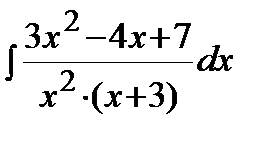 .
.
Решение. Подынтегральная дробь является правильной, так как степень многочлена в числителе меньше, чем в знаменателе. Разложим дробь на простейшие:
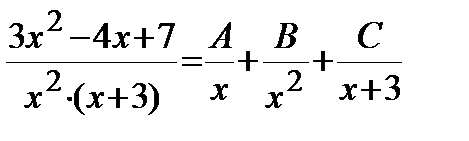 .
.
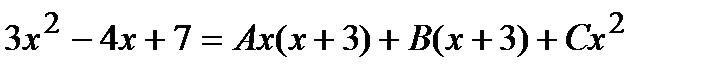 .
.
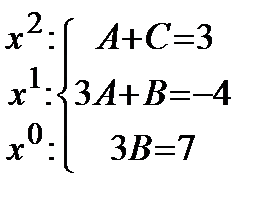 .
.
Решая систему, получим: 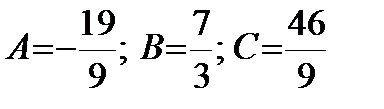 .
.
Тогда исходный интеграл примет вид:
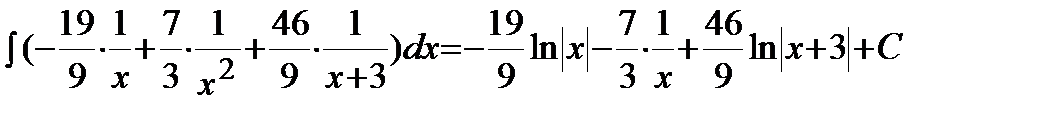 .
.
Интегрирование тригонометрических выражений.
Пример. 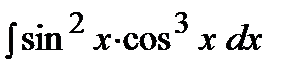 .
.
Решение.
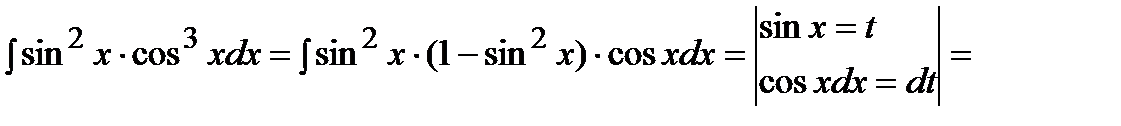
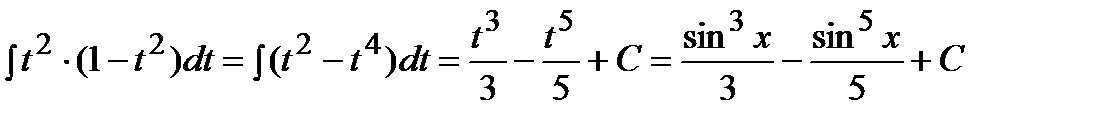 .
.
б) Оба числа m, n - четные неотрицательные.
Применим формулы:
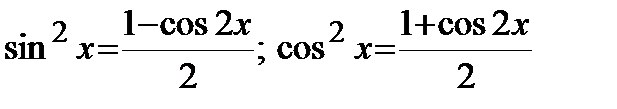 .
.
Пример. 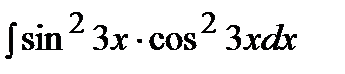 .
.
Решение.
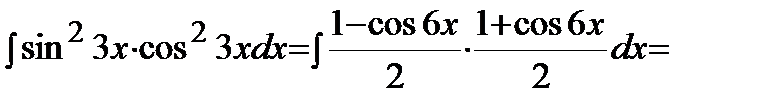
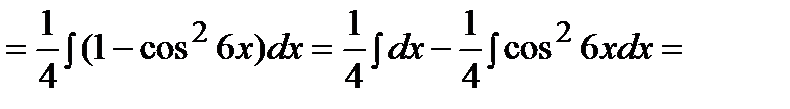
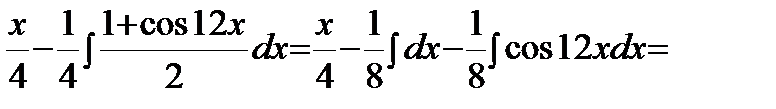
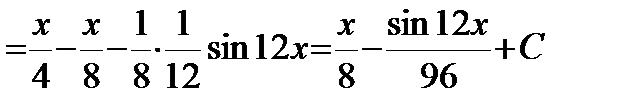 .
.
 2015-04-12
2015-04-12 556
556








