Пример. 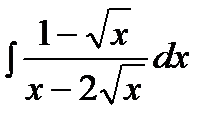 .
.
Решение. Сделаем замену 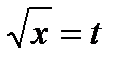 , откуда
, откуда 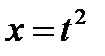 ,
, 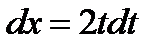 . В результате получим:
. В результате получим:
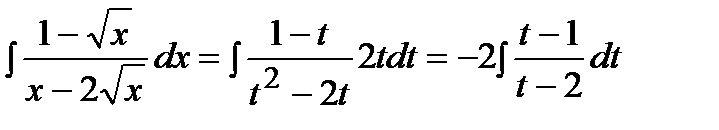 .
.
Исходный интеграл сведен к интегралу от рациональной функции – неправильной дроби, которую интегрируем с помощью выделения ее целой части:
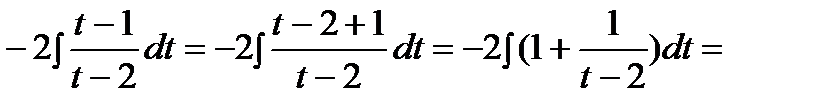
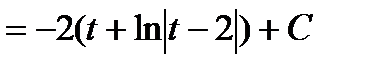 .
.
Таким образом, 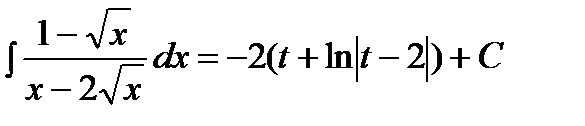 , где
, где 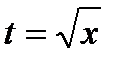 .
.
ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ И ЕГО ПРИЛОЖЕНИЯ
Если 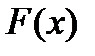 — некоторая первообразная функции
— некоторая первообразная функции 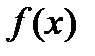 , непрерывной на отрезке
, непрерывной на отрезке 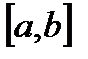 , то определенный интеграл вычисляется по формуле Ньютона – Лейбница:
, то определенный интеграл вычисляется по формуле Ньютона – Лейбница:
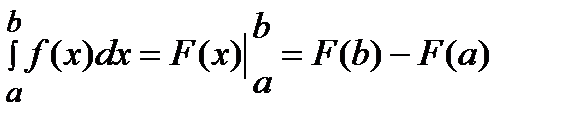 .
.
Пример. 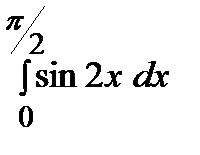 .
.
Решение.
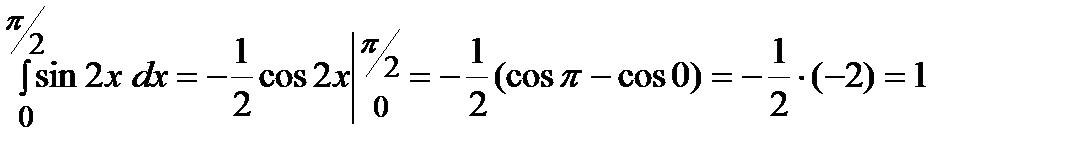 .
.
 2015-04-12
2015-04-12 652
652








