Вычисление площади плоской фигуры, ограниченной линиями, заданными в декартовых координатах

В декартовой системе координат элементарной фигурой является криволинейная трапеция (рис.1), ограниченная линиями 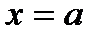, , 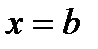, , 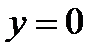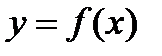площадь которой вычисляется по формуле:

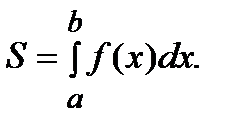
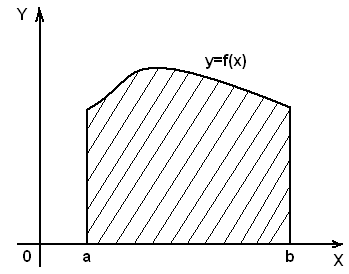
Рис.1

Площадь фигуры (рис.2) вычисляется по формуле:

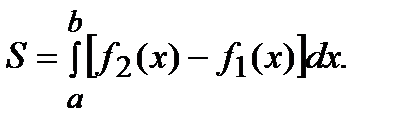
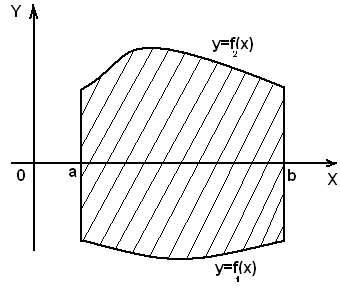
Рис.2

Пример. Найти площадь фигуры, ограниченной линиями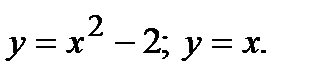

Решение. Построим чертеж к задаче (рис. 3).

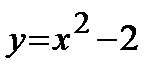— это парабола (ветви направлены вверх, вершина находится в точке с координатами (0;-2));

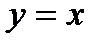— прямая, проходящая через начало координат.

Найдем точки пересечения кривых. Для этого решим систему уравнений: .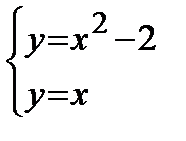

Отсюда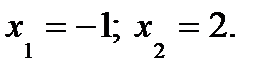

Площадь фигуры вычислим по формуле:

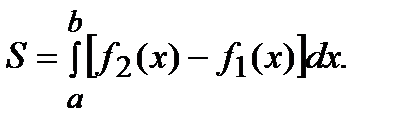
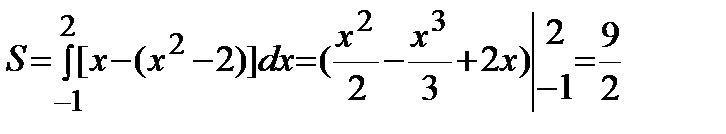(кв.ед.).

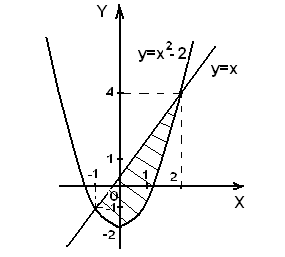
Рис. 3