Очевидно, что векторы стоящие в обеих частях второго свойства дистрибутивности

коллинеарны. Допустим сначала, что знаки λ и μ одинаковы. Тогда

векторы 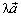и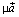

направлены одинаково и длина их суммы равна сумме их длин, т. е.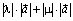

. Но 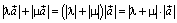и следовательно, в этом

случае векторы 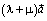и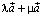

равны по длине. Направление их совпадает с направлением вектора

, если общий знак λ и μ положителен, и противоположно ему, если

отрицателен. Допустим теперь, что знаки λ и μ различны, и для

определенности будем считать |λ| > |μ|. В этом случае длина суммы

равна разности длин, точнее .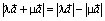

Но 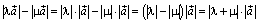. Следовательно, и в этом

случае длина вектор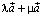а равна

длине вектора 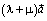. Очевидно, что

оба эти вектора направлены так же, как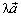

. Если же |λ| = |μ| и знаки λ и μ противоположны, то обе