2015-04-12
378
1. Из определения следует, что матрицы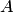 
и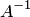 
перестановочны.
2. Матрица, обратная к невырожденной диагональной, является тоже диагональной:
3. Матрица, обратная к невырожденной нижней (верхней) треугольной, является нижней (верхней) треугольной.
4. Элементарные матрицы имеют обратные, которые также являются элементарными (см. п.1 замечаний 1.11).
Свойства обратной матрицы
Операция обращения матрицы обладает следующими свойствами:
если имеют смысл операции, указанные в равенствах 1-4.
Докажем свойство 2: если произведение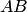 
невырожденных квадратных матриц одного и того же порядка имеет обратную матрицу, то 
.
Действительно, определитель произведения матриц 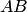не равен нулю, так как
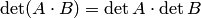, где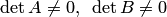 
Следовательно, обратная матрица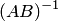 
существует и единственна. Покажем по определению, что матрица 
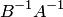является обратной по отношению к матрице 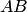. Действительно:
Из единственности обратной матрицы следует равенство . Второе свойство доказано. Аналогично доказываются и остальные свойства.
