2015-04-12
2130
Разберем решения нескольких примеров.
Пример.
Найдите решение неоднородной системы линейных алгебраических уравнений методом Крамера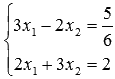 
.
Решение.
Основная матрица системы имеет вид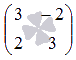 
. Вычислим ее определитель по формуле 
:
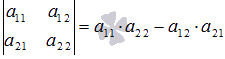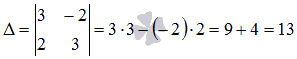
Так как определитель основной матрицы системы отличен от нуля, то СЛАУ имеет единственное решение, и оно может быть найдено методом Крамера. Запишем определител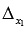и 
и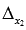 
. Заменяем первый столбец основной матрицы системы на столбец свободных членов, и получаем определитель 
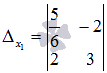. Аналогично заменяем второй столбец основной матрицы на столбец свободных членов, и получаем 
.
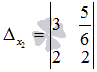Вычисляем эти определители:
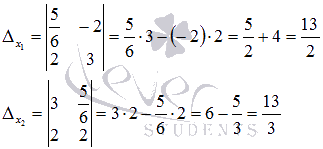
Находим неизвестные переменные x1 и x2 по формулам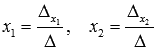 
:
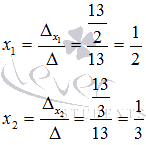
Выполним проверку. Подставим полученные значения x1 и x2 в исходную систему уравнений:
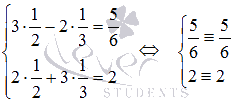
Оба уравнения системы обращаются в тождества, следовательно, решение найдено верно.
Ответ:
.
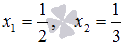Некоторые элементы основной матрицы СЛАУ могут быть равны нулю. В этом случае в уравнениях системы будут отсутствовать соответствующие неизвестные переменные. Разберем пример.
Пример.
Найдите решение системы линейных уравнений методом Крамера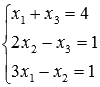 
.
Решение.
Перепишем систему в виде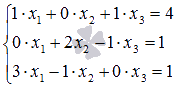 
, чтобы стало видно основную матрицу системы 
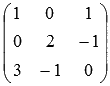. Найдем ее определитель по формуле
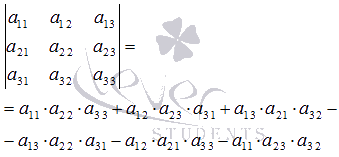
Имеем
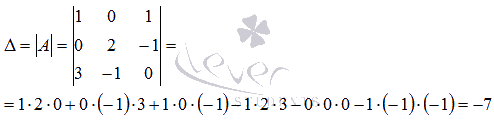
Определитель основной матрицы отличен от нуля, следовательно, система линейных уравнений имеет единственное решение. Найдем его методом Крамера. Вычислим определители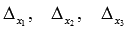 
:
Таким образом,
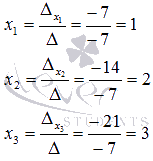
Ответ:
.
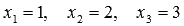Обозначения неизвестных переменных в уравнениях системы могут отличаться от x1, x2, …, xn. Это не влияет на процесс решения. А вот порядок следования неизвестных переменных в уравнениях системы очень важен при составлении основной матрицы и необходимых определителей метода Крамера. Поясним этот момент на примере.
Пример.
Используя метод Крамера, найдите решение системы трех линейных алгебраических уравнений с тремя неизвестными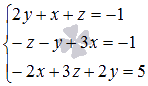 
.
Решение.
В данном примере неизвестные переменные имеют другое обозначение (x, y и z вместо x1, x2 и x3). Это не влияет на ход решения, но будьте внимательны с обозначениями переменных. В качестве основной матрицы системы НЕЛЬЗЯ брать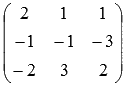 
. Необходимо сначала упорядочить неизвестные переменные во всех уравнениях системы. Для этого перепишем систему уравнений как 
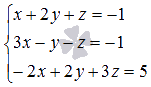. Теперь основную матрицу системы хорошо видно 
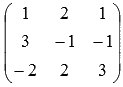. Вычислим ее определитель:
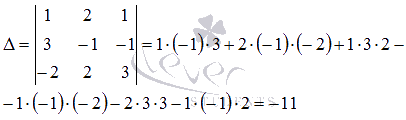
Определитель основной матрицы отличен от нуля, следовательно, система уравнений имеет единственное решение. Найдем его методом Крамера. Запишем определители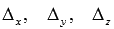 
(обратите внимание на обозначения) и вычислим их:
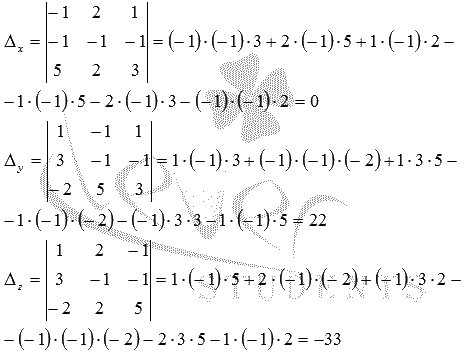
Осталось найти неизвестные переменные по формулам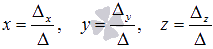 
:
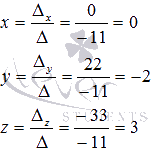
Выполним проверку. Для этого умножим основную матрицу на полученное решение 
(при необходимости смотрите раздел операции над матрицами):
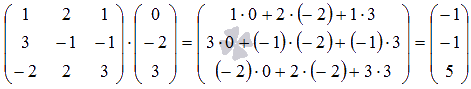
В результате получили столбец свободных членов исходной системы уравнений, поэтому решение найдено верно.
Ответ:
x = 0, y = -2, z = 3.
