Теорема. Если задана точка М(х0, у0), то расстояние до прямой Ах + Ву + С =0 определяется как
Доказательство. Пусть точка М1(х1, у1) – основание перпендикуляра, опущенного из точки М на заданную прямую. Тогда расстояние между точками М и М1:
(1)
Координаты x1 и у1 могут быть найдены как решение системы уравнений:
Второе уравнение системы – это уравнение прямой, проходящей через заданную точку М0перпендикулярно заданной прямой.
Если преобразовать первое уравнение системы к виду:
A(x – x0) + B(y – y0) + Ax0 + By0 + C = 0,
то, решая, получим:
Подставляя эти выражения в уравнение (1), находим:
Угол 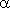 между прямыми:
между прямыми:
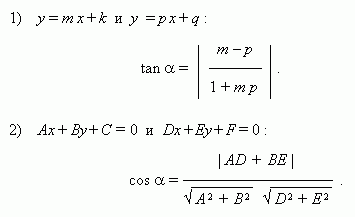
| Даны уравнения двух прямых. Требуется найти угол между ними. Угол между двумя непараллельными прямыми α1 и α2 найдем как угол между направляющими векторами этих прямых при задании канонических уравнений для α1 и α2, или же как угол между их нормалями, если заданы общие уравнения прямых α1 и α2. |
Пусть заданы две прямые α1: 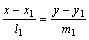 и α2:
и α2: 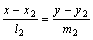 .
.
Направляющие векторы этих прямых: 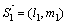 и
и 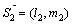 .
.
Угол φ между прямыми найдем из скалярного произведения векторов 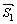 и
и 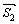 :
: 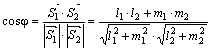 .
.
Пусть заданы общие уравнения прямых 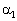 и
и 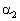 : А 1 х+В 1 у+С 1 = 0 и А 2 х+В 2 у+С 2=0. Тогда нормали к этим прямым:
: А 1 х+В 1 у+С 1 = 0 и А 2 х+В 2 у+С 2=0. Тогда нормали к этим прямым: 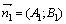 и
и 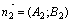 , и
, и  .
.
Если 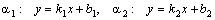 , то из
, то из 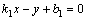 и
и 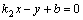 следует:
следует: 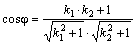 .
.
Условием перпендикулярности прямых будет соответственно:
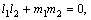 либо
либо 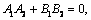 либо
либо 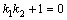 .
.
Из последнего равенства следует, что 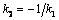 . Таким образом угловые коэффициенты двух перпендикулярных прямых обратные по величине и противоположны по знаку.
. Таким образом угловые коэффициенты двух перпендикулярных прямых обратные по величине и противоположны по знаку.
Условием параллельности прямых будет соответствовать:
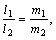 либо
либо 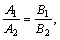 либо
либо 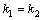 .
.
 2015-04-12
2015-04-12 857
857









