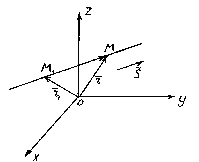 Положение прямой в пространстве вполне определяется заданием какой-либо её фиксированной точки М 1 и вектора
Положение прямой в пространстве вполне определяется заданием какой-либо её фиксированной точки М 1 и вектора 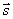 , параллельного этой прямой.
, параллельного этой прямой.
Вектор 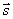 , параллельный прямой, называется направляющим вектором этой прямой.
, параллельный прямой, называется направляющим вектором этой прямой.
Итак, пусть прямая l проходит через точку М 1(x 1, y 1, z 1), лежащую на прямой параллельно вектору 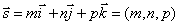 .
.
Рассмотрим произвольную точку М(x,y,z) на прямой. Из рисунка видно, что 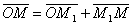 .
.
Векторы 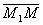 и
и 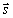 коллинеарны, поэтому найдётся такое число t, что
коллинеарны, поэтому найдётся такое число t, что 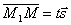 , где множитель t может принимать любое числовое значение в зависимости от положения точки M на прямой. Множитель t называется параметром. Обозначив радиус-векторы точек М 1 и М соответственно через
, где множитель t может принимать любое числовое значение в зависимости от положения точки M на прямой. Множитель t называется параметром. Обозначив радиус-векторы точек М 1 и М соответственно через 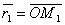 и
и 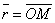 , получаем
, получаем 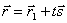 . Это уравнение называется векторным уравнением прямой. Оно показывает, что каждому значению параметра t соответствует радиус-вектор некоторой точки М, лежащей на прямой.
. Это уравнение называется векторным уравнением прямой. Оно показывает, что каждому значению параметра t соответствует радиус-вектор некоторой точки М, лежащей на прямой.
Запишем это уравнение в координатной форме. Заметим, что 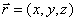 ,
, 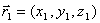 и
и 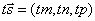 отсюда
отсюда 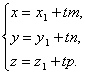
Полученные уравнения называются параметрическими уравнениями прямой.
При изменении параметра t изменяются координаты x, y и z и точка М перемещается по прямой.
Пример 13
Составить параметрические уравнения прямой по точке 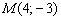 и направляющему вектору
и направляющему вектору 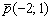
Решение закончилось, не успев начаться:
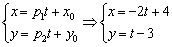
Параметр «тэ» может принимать любые значения от «минус бесконечности» до «плюс бесконечности», и каждому значению параметра соответствует конкретная точка плоскости. Например, если 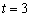 , то получаем точку
, то получаем точку 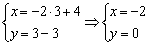 .
.
Обратная задача: как проверить, будет ли точка 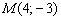 условия принадлежать данной прямой?
условия принадлежать данной прямой?
Подставим координаты точки 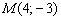 в полученные параметрические уравнения:
в полученные параметрические уравнения:
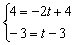
Из обоих уравнений следует, что  , то есть, система совместна и имеет единственное решение.
, то есть, система совместна и имеет единственное решение.
Рассмотрим более содержательные задания:
Пример 14
Составить параметрические уравнения прямой 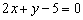
Решение: По условию прямая задана в общем виде. Для того чтобы составить параметрические уравнения прямой, нужно знать её направляющий вектор и какую-нибудь точку, принадлежащую данной прямой.
Найдём направляющий вектор: 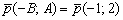
Теперь нужно найти какую-нибудь точку, принадлежащую прямой (подойдёт любая), в этих целях общее уравнение удобно переписать в виде уравнения с угловым коэффициентом: 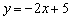
Напрашивается, конечно, точка 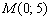
Составим параметрические уравнения прямой:
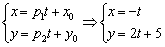
Ответ: 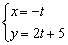
 2015-04-12
2015-04-12 4842
4842
