Прежде чем приступить к нахождению уравнения прямой, проходящей через заданную точку перпендикулярно заданной прямой, обговорим некоторые важные моменты.
В средней школе на уроках геометрии доказывается следующая теорема: через заданную точку плоскости можно провести единственную прямую, перпендикулярную заданной прямой. Однако, через заданную точку трехмерного пространства можно провести бесконечно много прямых, перпендикулярных заданной прямой. Действительно, если построить плоскость  , проходящую через заданную точку M1 перпендикулярно к заданной прямой b, то любая прямая, лежащая в этой плоскости и проходящая через заданную точку M1, перпендикулярна заданной прямой b.
, проходящую через заданную точку M1 перпендикулярно к заданной прямой b, то любая прямая, лежащая в этой плоскости и проходящая через заданную точку M1, перпендикулярна заданной прямой b.
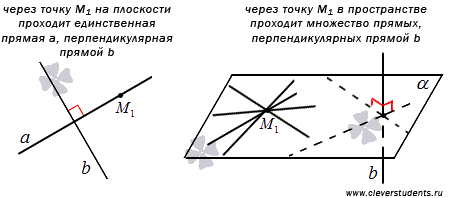
Таким образом, задача о составлении уравнения прямой, проходящей через заданную точку перпендикулярно заданной прямой, имеет практическое значение лишь для случая на плоскости.
В трехмерном пространстве обычно ищут уравнение плоскости, проходящей через заданную точку перпендикулярно к заданной прямой.
|
|
|
Итак, пусть на плоскости зафиксирована прямоугольная декартова система координат Oxyz, задана прямая b, которой в этой системе координат соответствует уравнение прямой на плоскости некоторого вида, задана точка 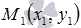 , и требуется написать уравнение прямой a, проходящей через точку M1 перпендикулярно прямой b.
, и требуется написать уравнение прямой a, проходящей через точку M1 перпендикулярно прямой b.
Обсудим способы решения этой задачи.
Из условия нам известны координаты точки М1, лежащей на прямой a, уравнение которой нам предстоит составить. Но этого мало. Чтобы написать уравнение прямой a, нам нужно знать еще или координаты направляющего вектора прямой a, или координаты нормального вектора прямой a, или угловой коэффициент прямой a. Откуда нам получить эти данные? Ответ очевиден - из заданного уравнения прямой b. Так как прямые b и a перпендикулярны по условию, то направляющий вектор прямой b является нормальным вектором прямой a, нормальный вектор прямой b является направляющим вектором прямой a, а угловые коэффициенты 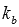 и
и 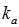 прямых b и a соответственно связаны соотношением
прямых b и a соответственно связаны соотношением 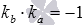 (это мы обсуждали в статье перпендикулярные прямые, перпендикулярность прямых).
(это мы обсуждали в статье перпендикулярные прямые, перпендикулярность прямых).
Итак, пусть мы нашли направляющий вектор прямой b вида 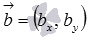 , тогда нормальным вектором прямой a является вектор
, тогда нормальным вектором прямой a является вектор 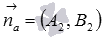 , где
, где 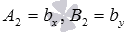 , следовательно, мы можем записать общее уравнение прямой a, которая проходит через точку
, следовательно, мы можем записать общее уравнение прямой a, которая проходит через точку 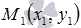 и имеет нормальный вектор
и имеет нормальный вектор 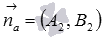 , в виде
, в виде 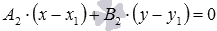 .
.
Если мы определили нормальный вектор прямой b вида 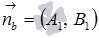 , то направляющий вектор прямой a есть вектор
, то направляющий вектор прямой a есть вектор 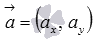 , где
, где 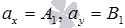 , следовательно, мы можем составить каноническое уравнение прямой a или параметрические уравнения прямой a, которая проходит через точку
, следовательно, мы можем составить каноническое уравнение прямой a или параметрические уравнения прямой a, которая проходит через точку 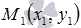 и имеет направляющий вектор
и имеет направляющий вектор 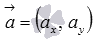 , в виде
, в виде 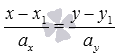 или
или 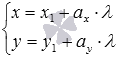 соответственно.
соответственно.
|
|
|
Если же мы нашли угловой коэффициент 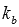 прямой b, то угловой коэффициент прямой a равен
прямой b, то угловой коэффициент прямой a равен 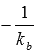 , следовательно, мы можем написать уравнение прямой a, проходящей через точку
, следовательно, мы можем написать уравнение прямой a, проходящей через точку 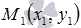 и имеющей угловой коэффициент
и имеющей угловой коэффициент 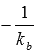 , в виде
, в виде 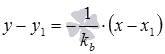 (об этом написано в статье уравнение прямой с угловым коэффициентом).
(об этом написано в статье уравнение прямой с угловым коэффициентом).
От найденного уравнения прямой, проходящей через заданную точку плоскости перпендикулярно заданной прямой, можно при необходимости перейти к другому виду уравнения этой прямой.
Пример.
Напишите уравнение прямой a, которая в прямоугольной системе координат Oxy на плоскости проходит через точку 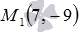 и перпендикулярна прямой b, заданной каноническим уравнением прямой
и перпендикулярна прямой b, заданной каноническим уравнением прямой 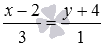 .
.
Решение.
Очевидно, что 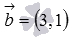 - направляющий вектор прямой
- направляющий вектор прямой 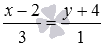 . Так как прямая a перпендикулярна прямой b, то координаты вектора
. Так как прямая a перпендикулярна прямой b, то координаты вектора 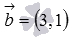 являются координатами нормального вектора прямой a, то есть,
являются координатами нормального вектора прямой a, то есть, 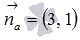 . Уравнение прямой, проходящей через точку
. Уравнение прямой, проходящей через точку 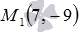 и имеющей нормальный вектор
и имеющей нормальный вектор 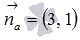 , записывается в виде
, записывается в виде 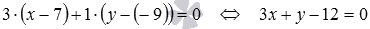 . Это и есть искомое уравнение прямой, проходящей через точку
. Это и есть искомое уравнение прямой, проходящей через точку 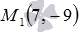 перпендикулярно прямой
перпендикулярно прямой 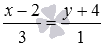 .
.
 2015-04-12
2015-04-12 1907
1907
