Уравнения второго порядка от двух переменных
Ax 2 + 2 Bxy + Cy 2 + 2 Dx + 2 Ey + F = 0
описывают конические сечения или кривые второго порядка на плоскости – окружность, эллипс, параболу, гиперболу. Построим канонические уравнения этих кривых по алгоритму
Окружность
|
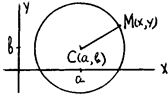 2) Общее свойство точек окружности | CM | = R.
2) Общее свойство точек окружности | CM | = R. 3) Переход к координатной форме общего свойства
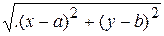 = R,
= R,
(x – a)2 + (y – b)2 = R 2. (34)
Эллипс
Определение. Эллипс образуют точки плоскости, для каждой из которых сумма расстояний от двух данных точек постоянна и больше расстояния между этими точками.
Данные точки – фокусы, расстояние между ними – фокальные расстояния.
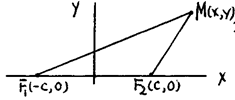
|
3) Переход к координатам
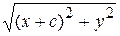 +
+ 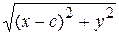 = 2 a,
= 2 a,
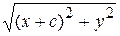 = 2 a –
= 2 a – 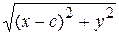

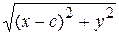 = a – (c / a) x
= a – (c / a) x 
 [(a 2 – c 2)/ a 2] x 2 + y 2 = a 2 – c 2.
[(a 2 – c 2)/ a 2] x 2 + y 2 = a 2 – c 2.
Пусть a 2 – c 2 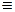 b 2, тогда получаем каноническое уравнение эллипса
b 2, тогда получаем каноническое уравнение эллипса
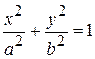 . (35)
. (35)
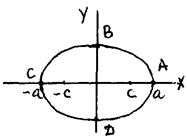 Точки А (а; 0), С (– а; 0), В (0; b), D (0; – b) – вершины эллипса, АС – большая ось, ВD – малая ось, а, в – полуоси. Отношение с / а =
Точки А (а; 0), С (– а; 0), В (0; b), D (0; – b) – вершины эллипса, АС – большая ось, ВD – малая ось, а, в – полуоси. Отношение с / а = 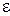 – эксцентриситет (0 <
– эксцентриситет (0 < 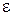 <1) определяет переход окружности в прямую линию. Оси координат являются осями симметрии эллипса, а их начало – центром симметрии. Координата фокуса
<1) определяет переход окружности в прямую линию. Оси координат являются осями симметрии эллипса, а их начало – центром симметрии. Координата фокуса
c = 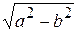 .
.
Параметрическое уравнение эллипса: x = a cos t, y = b sin t, 0 < t < 2  .
.
Пример. Наименьшее расстояние Земли от Солнца 147,5 млн. км, наибольшее – 152,5 млн. км. Найти большую полуось и эксцентриситет эллиптической орбиты Земли.
Решение: max = a + c = 152,5, min = a – c = 147,5  a = 150 млн. км,
a = 150 млн. км,
с = 2,5 млн. км, b = 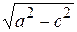 = 149,98 млн. км
= 149,98 млн. км 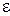 = c / a = 0,017, a – b = 20 т. км.
= c / a = 0,017, a – b = 20 т. км.
Пример. Расстояние между фокусами равно 8, а малая полуось равна 3. Написать уравнение эллипса.
Решение: т.к. 2с = 8 и b = 3, то c = 4, a = 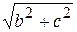 = 5,
= 5, 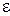 = c/a = 0,8,
= c/a = 0,8, 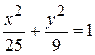 .
.
Гипербола
Определение. Гиперболу образуют точки плоскости для каждой из которых модуль разности расстояний до двух данных точек плоскости постоянен и меньше расстояния между этими точками.
Данные точки – фокусы, а расстояние между ними – фокальное расстояние.
|
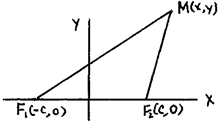 2) Общее свойство точек | F 1 M | – | F 2 M | = 2a.
2) Общее свойство точек | F 1 M | – | F 2 M | = 2a. 3) Переход к координатам дает каноническое уравнение гиперболы
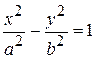 . (36)
. (36)
Гипербола имеет две ветви. Точки пересечения гиперболы с осью Ох называются вершинами гиперболы. А (а; 0) и В (– а; 0). Отрезок АВ – действительная ось гиперболы. Число а – действительная полуось гиперболы, в – мнимая полуось. Прямые с уравнениями y = b / a х и y = – b / a х называются асимптотами гиперболы. При х 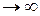 ветви гиперболы вплотную проходят вдоль этих прямых.
ветви гиперболы вплотную проходят вдоль этих прямых.
Оси координат являются осями симметрии гиперболы, а их начало – центром симметрии. Координата фокуса c = 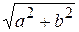 . Форму гиперболы характеризует эксцентриситет с / а =
. Форму гиперболы характеризует эксцентриситет с / а = 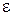 > 1. Чем
> 1. Чем 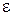 меньше, тем меньше угол между асимптотами, сжимающими ветвь гиперболы.
меньше, тем меньше угол между асимптотами, сжимающими ветвь гиперболы.
Алгоритм построения графика гиперболы
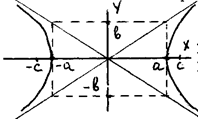 1.Через концы осей провести прямые параллельные осям координат.
1.Через концы осей провести прямые параллельные осям координат.
2. Провести диагонали прямоугольника и их продолжение.
3.От концов действительной оси в сторону асимптот провести сами кривые.
Пример. Даны: вещественная полуось a = 2 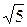 и эксцентриситет
и эксцентриситет
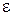 =
= 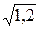 . Написать уравнение гиперболы.
. Написать уравнение гиперболы.
Решение: т.к. с = a 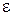 , то b =
, то b = 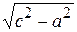 = a
= a 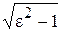 = 2 и
= 2 и 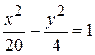 .
.
Парабола
Определение. Параболу образуют точки плоскости, для каждой из которых расстояние до данной точки равно расстоянию до данной прямой, не проходящей через данную точку.
Данная точка называется фокусом параболы, а данная прямая называется директрисой. Расстояние от фокуса до директрисы называется фокальным параметром и обозначается p. Уравнение директрисы x = – p /2.
|
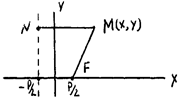 2) Общее свойство точек | MF | = | MN |.
2) Общее свойство точек | MF | = | MN |. 3) Переход к координатам
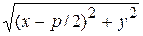 = x + p /2
= x + p /2  y 2 = 2 px.
y 2 = 2 px.
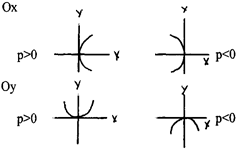 Каноническое уравнение параболы имеет 2 вида:
Каноническое уравнение параболы имеет 2 вида:
y 2 = 2 px – симметрия относительно
x 2 = 2 py – симметрия относительно
 2015-04-12
2015-04-12 1424
1424
