Общее уравнение кривых второго порядка

Общее уравнение кривой второго порядка на плоскости имеет вид:

Ax ² + 2 Bxy + Cy ² + 2 Dx + 2 Ey + F = 0, (39)

где A ² + B ² + C ² 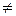0, (A, B, C, D, E, F) 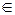R. Оно определяет все возможные конические сечения произвольным образом расположенные на плоскости.

Из коэффициентов уравнения (39) составим два определителя:

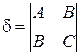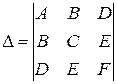, , (40)

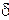– называется дискриминантом уравнения (39), а 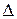– дискриминантом старших членов уравнения. При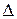 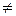0 уравнение (39) определяет: 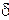> 0 – эллипс; 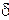< 0 – гиперболу; 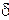= 0 – параболу. В случае 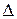= 0 кривые вырождаются в точку или прямые линии.

От общего уравнения (39) можно перейти к каноническому уравнению, если исключить линейные и перекрестный члены путем перехода в новую систему координат, совпадающую с осями симметрии фигуры. Заменим в (39) x на x + a и y на y + b, где a, b некоторые константы. Выпишем полученные коэффициенты при х и y и приравняем их к 0

(Aa + Bb + D) x = 0, (Cb + Ba + E) y = 0. (41)

В результате уравнение (39) примет вид:

A (x)² + 2 B (x)(y) + C (y)² + F = 0, (42)

где коэффициенты А, B, C не изменились, а F = 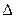/ 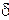. Решение системы уравнений (41) определит координаты центра симметрии фигуры:

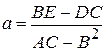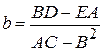, . (43)

Если B = 0, то a = – D / A, b = – E / C и исключать линейные члены в (39) удобно методом приведения к полному квадрату:

Ax ² + 2 Dx = A (x ² + 2 xD / A + (D / A)² – (D / A)²) = A (x + D / A)² – D ²/ A.

В уравнении (42) совершим поворот координат на угол a (38). Выпишем полученный коэффициент при перекрестном члене xy и приравняем его к 0

[sin2 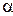(A–C) + 2cos2 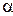B ] xy = 0. (44)

Условие (44) определяет необходимый угол поворота осей координат до их совпадения с осями симметрии фигуры и принимает вид:

tg2 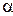= 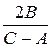. (45)

Уравнение (42) принимает форму:

A ⁺X² + C ⁺ Y ² + F = 0 (46)

от которой легко перейти к каноническому уравнению кривой:

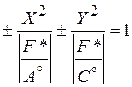. (47)

Коэффициенты A ⁺, C ⁺, при условии (45), можно представить как корни вспомогательного квадратного уравнения:

t ² – (A + C) t + 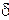= 0. (48)

В результате определены положение и направление осей симметрии фигуры, ее полуоси:

a² = 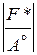, b² =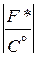

и она может быть построена геометрически.

В случае 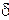= 0 имеем параболу. Если её ось симметрии параллельна оси Ох, то уравнение сводится к виду:

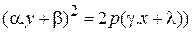, (49)

если нет, то к виду:

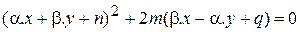, (50)

где выражения в скобках, приравненные к 0, определяют линии новых осей координат: , .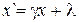

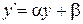Решение типичных задач

Пример 15. Привести уравнение 2 x ² + 3 y ² – 4 x + 6 y – 7 = 0 к каноническому виду и построить кривую.

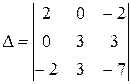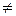Решение. B = 0, = –72 0, 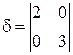= 6 > 0 эллипс.

Выполним приведение к полному квадрату:

2(x – 1)² + 3(y + 1)² – 12 = 0.

Координаты центра симметрии (1; –1), линейное преобразование X = x – 1, Y = y + 1 приводит уравнение к каноническому виду .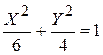

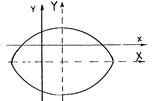
Пример 16. Привести уравнение 2 xy = a ² к каноническому виду и построить кривую.

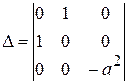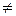Решение. B = 1, = a ² 0, 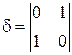= –1 < 0 гипербола.

Центр системы координат находится в центре симметрии кривой, т.к. в уравнении нет линейных членов. Совершим поворот осей на угол a. По формуле (45) имеем tg2a = B /(A – C) = 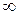, т.е. a = 45°. Коэффициенты канонического уравнения (46) A ⁺, C ⁺ определяются уравнением (48): t ² = 1 или t _1,2 = 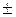1 A ⁺ = 1, C ⁺ = –1, т.е.
X ² – Y ² = a ² или 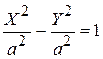. Таким образом, уравнение 2 ху = а ² описывает гиперболу с центром симметрии в (0; 0). Оси симметрии располагаются по биссектрисам координатных углов, асимптотами служат оси координат, полуоси гиперболы равны а.

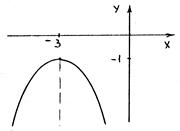
Пример 17. Привести уравнение x ² + 6 х + y + 10 = 0 к каноническому виду и построить кривую.

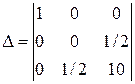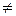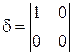Решение. B = 0, = –¼ 0, = 0 парабола.

Выполним приведение к полному квадрату:

(x + 3)² = –(y + 1).

Координаты центра симметрии (–3; –1), линейное преобразование
X = x + 3, Y = y + 1 приводит уравнение к каноническому виду X ² = – Y, где фокальный параметр р = 1/2.

Задачи для самостоятельного решения

Привести к каноническому виду следующие уравнения и построить соответствующие кривые:

- 4 x ² + 9 y ² – 16 x – 18 y – 11 = 0;

- x ² + 2 х – y = 0;

- x ² – 9 y ² + 6 x + 18 y – 9 =0;

- 9 x ² + y ² – 18 x + 2 y + 1 = 0;

- 2 x ² + 4 х + y – 2 = 0;

- 3 x ² – 6 х – y + 2 = 0;

- x ² + 4 y ² – 8 x – 9 y + 16 = 0;

- 4 x ² + 8 х – y – 5 = 0;

- 9 x ² – y ² + 18 x + 2 y – 1 = 0;

- 9 x ² – 4 y ² + 36 x + 16 y – 16 = 0.