Определение. Любой вектор, отличный от нулевого, параллельный заданной прямой, называется направляющим вектором этой прямой.
Пусть на прямой 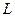 задана точка
задана точка 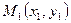 , а вектор
, а вектор 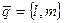 – направляющий вектор прямой
– направляющий вектор прямой 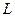 . Точка
. Точка 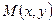 принадлежит прямой, если вектор
принадлежит прямой, если вектор 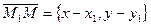 параллелен вектору
параллелен вектору 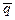 :
:
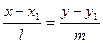 . (12)
. (12)
Уравнение (12) называется каноническим уравнением прямой на плоскости.
Угол между прямыми, заданными каноническими уравнениями, определяется как угол между направляющими векторами этих прямых:
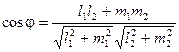 .
.
Условием параллельности прямых будет условие коллинеарности их направляющих векторов:
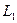 ||
|| 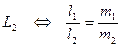 .
.
Условие перпендикулярности прямых равносильно условию равенства нулю скалярного произведения их направляющих векторов:
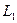 ^
^ 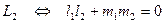 .
.
 2015-04-12
2015-04-12 495
495








