Определение. Совокупность всех прямых, проходящих через некоторую точку S (х0, у0), называется пучком прямых с центром S.
Теорема. Пусть 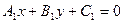 и
и 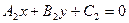 – уравнения двух прямых, пересекающихся в точке S,
– уравнения двух прямых, пересекающихся в точке S,
α и β – числа не равные нулю одновременно. Тогда
α(А1х + В1у + С1) + β(А2х + В2у + С2) = 0 (*)
– это уравнение прямой, проходящей через точку S.
Доказательство.
Докажем, что соотношение (*) является уравнением 1-ой степени.
Запишем его в виде
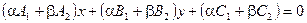
и покажем, что 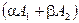 и
и 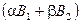 не обращаются в ноль одновременно.
не обращаются в ноль одновременно.
Докажем от противного: пусть 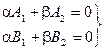 . Тогда
. Тогда
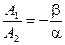 и
и 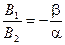 .
.
Следовательно, 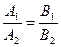 . Но этого не может быть, т. к. по условию прямые пересекаются. Наше предположение оказалось неверно,
. Но этого не может быть, т. к. по условию прямые пересекаются. Наше предположение оказалось неверно, 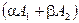 и
и 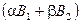 не равны нулю одновременно, т. е. равенство (*) – уравнение с двумя переменными (х,у). Это уравнение 1-ой степени, которое определяет прямую.
не равны нулю одновременно, т. е. равенство (*) – уравнение с двумя переменными (х,у). Это уравнение 1-ой степени, которое определяет прямую.
Остается доказать, что эта прямая проходит через точку S. Пусть х0, у0 – координаты точки S. Они удовлетворяют каждому из двух уравнений прямых, следовательно, для любых значений 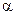 и
и 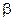 выполняется равенство
выполняется равенство
α(А1х0 + В1у0 + С1) + β(А2х0 + В2у0 + С2) = 0. (**)
Значит, все прямые, определяемые уравнением (*) при различных значениях 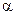 и
и 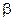 , проходят через точку S. Теорема доказана.
, проходят через точку S. Теорема доказана.
Пусть требуется найти прямую пучка (*), проходящую через заданную точку М *(х*, у *). Должно выполняться равенство
α (А1х*+В1у*+С1) + β (А2х*+В2у*+С2) = 0.
Для любого значения 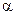
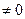 можно принять
можно принять 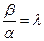 . Тогда из уравнения
. Тогда из уравнения
А1х*+В1у*+С1 + λ (А2х*+В2у*+С2) = 0 можно найти 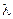 , а уравнение
, а уравнение
А1х+В1у+С1 + λ (А2х+В2у+С2) = 0 определяет искомую прямую.
 2015-04-12
2015-04-12 888
888








