2015-04-12
627
1. Векторное произведение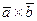 
равно нулю тогда и только тогда, когда эти векторы коллинеарны:
|| 
.
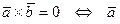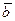Доказательство. Пусть угол между векторами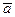 
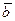и равен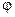 
.
a) Докажем, что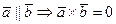 
.
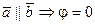или 
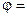1800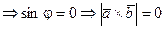 
.
б) Докажем, что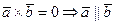 
.
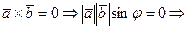
если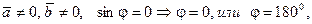 
Þ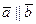 
.
Если 
, или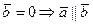 
. 
2. Модуль векторного произведения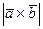 
равен площади параллелограмма, построенного на этих векторах.
Доказательство. Из курса геометрии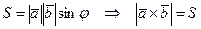 
Из свойства 2 следует, что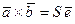 
, где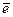 
– единичный вектор, перпендикулярный векторам 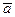и 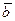и образующий с ними правую тройку:
а)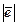 
=1,
б)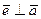 
, 
,
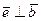в)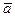 
, 
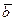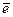, – правая тройка.
