Векторная алгебра
Пример 1. Дана точка 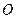 пересечения диагоналей параллелограмма
пересечения диагоналей параллелограмма 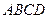 и векторы
и векторы 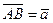 ,
, 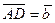 . Выразить через
. Выразить через 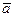 и
и 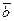 векторы
векторы 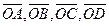 .
.
Решение. В соответствии с определением суммы и разности векторов имеем (рис. 3.1).
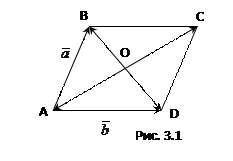
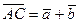 ,
, 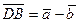 . Исходя из свойства диагоналей параллелограмма и определения произведения вектора на число, находим
. Исходя из свойства диагоналей параллелограмма и определения произведения вектора на число, находим
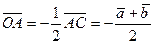 ;
; 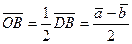 ;
;
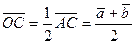 ;
; 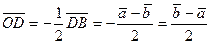 .
.
Пример 2. Два ненулевых вектора 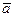 и
и 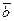 таковы, что
таковы, что 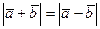 . Доказать, что векторы
. Доказать, что векторы 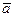 и
и 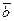 перпендикулярны.
перпендикулярны.
Решение. Построим на векторах 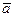 и
и 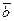 параллелограмм
параллелограмм 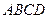 (рис. 3.1). Тогда
(рис. 3.1). Тогда 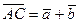 ,
, 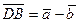 .
.
Равенство 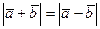 означает, что длины диагоналей параллелограмма равны, то есть
означает, что длины диагоналей параллелограмма равны, то есть 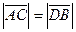 . Значит, данный параллелограмм есть прямоугольник. Следовательно, векторы
. Значит, данный параллелограмм есть прямоугольник. Следовательно, векторы 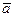 и
и 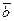 перпендикулярны.
перпендикулярны.
Пример 3. На стороне 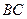 треугольника
треугольника 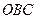 расположена точка
расположена точка 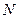 так, что
так, что 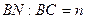 (рис. 3.2). Разложить вектор
(рис. 3.2). Разложить вектор 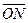 по векторам
по векторам 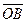 и
и 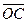 .
.
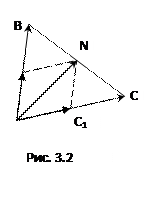
| Решение.
Для геометрического решения задачи достаточно из конца вектора 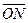 провести прямые, параллельные векторам провести прямые, параллельные векторам 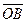 и и 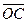 . В полученном параллелограмме . В полученном параллелограмме 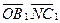 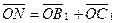 , , 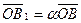 и и 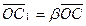 , т.е. , т.е. 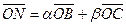 , однако коэффициенты , однако коэффициенты 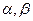 этого разложения геометрическим способом определяются лишь приближенно.
Решим задачу аналитическим методом. этого разложения геометрическим способом определяются лишь приближенно.
Решим задачу аналитическим методом.
|
Векторы 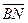 и
и 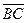 коллинеарны и одинаково направлены.
коллинеарны и одинаково направлены.
По условию 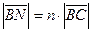 , значит
, значит 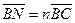 .
.
Так как 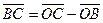 и
и 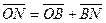 , то
, то 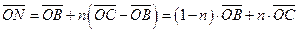 . Значит
. Значит 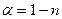 ,
, 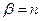 .
.
Если 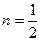 , то точка
, то точка 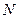 является серединой стороны
является серединой стороны 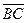 , а
, а 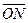 - медианой треугольника. В этом случае
- медианой треугольника. В этом случае
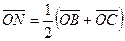 .
.
Пример 4. Дана треугольная призма 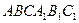 (рис. 3.3). Разложить вектор
(рис. 3.3). Разложить вектор 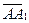 по векторам
по векторам 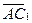 ,
, 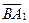 и
и 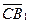 .
.
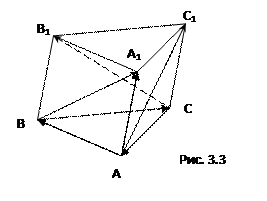
Решение. Согласно правилу треугольника сложения векторов имеем
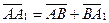 ,
,
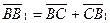 ,
,
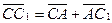 .
.
Складывая левые и правые части этих векторных равенств, получаем:
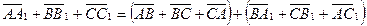 .
.
Так как
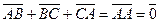 ,
,
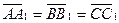 , то
, то 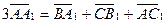 ,
,
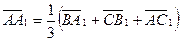 .
.
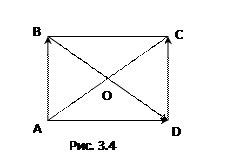
Пример 5. В прямоугольнике 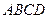 (рис. 3.4)
(рис. 3.4) 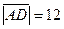 ,
, 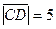 ,
,
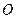 - точка пересечения диагоналей. Найдите
- точка пересечения диагоналей. Найдите 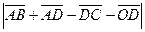 .
.
Решение. 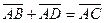 ,
, 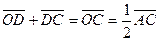 .
.
Значит, 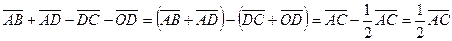 .
.
Найдем 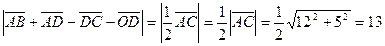 .
.
Пример 6. Векторы 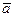 и
и 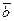 неколлинеарны. Найти, при каком
неколлинеарны. Найти, при каком 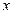 векторы
векторы 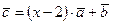 и
и 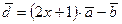 будут коллинеарны.
будут коллинеарны.
Решение. Вектор 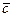 ненулевой, следовательно, существует такое число
ненулевой, следовательно, существует такое число 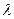 , что
, что
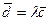 или
или 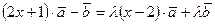 .
.
Откуда 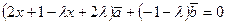 .
.
Векторы 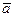 и
и 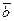 неколлинеарны, поэтому
неколлинеарны, поэтому
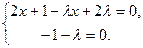
Решая эту систему, находим 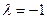 ,
, 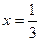 .
.
При 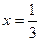
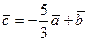 ,
, 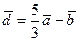 . Значит,
. Значит, 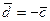 .
.
 2015-04-12
2015-04-12 468
468







