Пример 1. Найти объем параллелепипеда, построенного на векторах 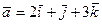 ,
, 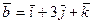 ,
, 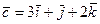 .
.
Решение. Найдем смешанное произведение векторов 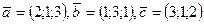 . Согласно формуле (3.35) имеем:
. Согласно формуле (3.35) имеем:
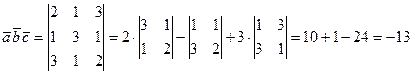 .
.
Найдем объем параллелепипеда по формуле (3.36)
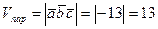 .
.
Пример 2. Проверить, компланарны ли векторы 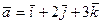 ,
, 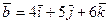 и
и 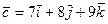 .
.
Решение. Воспользуемся свойством 4 смешанного произведения. Найдем 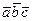 трех векторов с координатами
трех векторов с координатами 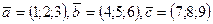 .
.
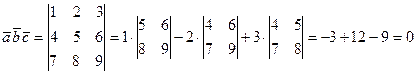
Значит векторы 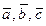 компланарны.
компланарны.
Пример 3. Доказать, что точки 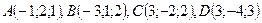 лежат в одной плоскости.
лежат в одной плоскости.
Решение. Достаточно показать, что три вектора 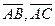 и
и 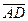 компланарны. Найдем координаты векторов
компланарны. Найдем координаты векторов
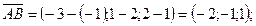
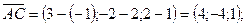
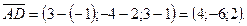
Проверим условие компланарности векторов
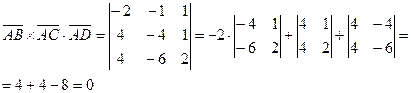
Значит, векторы 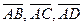 компланарны, а точки
компланарны, а точки 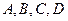 лежат в одной плоскости.
лежат в одной плоскости.
Пример 4. Дана пирамида с вершинами 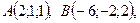
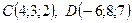 .
.
Вычислить длину высоты, опущенной из вершины 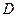 .
.
Решение. Используем известную формулу 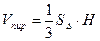 , откуда
, откуда 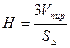 . Для нахождения
. Для нахождения 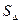 и
и 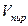 воспользуемся свойствами векторного и смешанного произведения векторов
воспользуемся свойствами векторного и смешанного произведения векторов
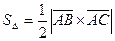 ,
, 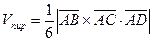 .
.
Вычислим координаты векторов и их произведения:
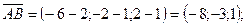
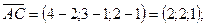
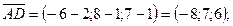
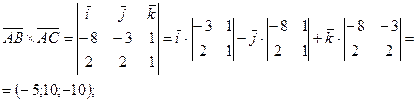
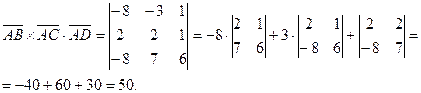
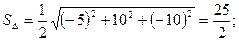
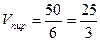 .
.
Высота пирамиды:
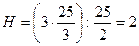 .
.
 2015-04-12
2015-04-12 546
546








