· Основные определения
Определение 1.1. Матрицей размера 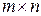 называется прямоугольная таблица чисел:
называется прямоугольная таблица чисел:
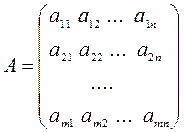 .
.
Каждый элемент матрицы 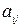 имеет два индекса: i – номер строки и j – номер столбца.
имеет два индекса: i – номер строки и j – номер столбца.
ü Матрица, состоящая из одних нулей, называется нулевой и обозначается O.
ü Матрица, у которой все элементы главной диагонали равны единице (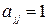 ), а все остальные элементы – нули, называется единичной и обозначается E.
), а все остальные элементы – нули, называется единичной и обозначается E.
ü Матрица, в которой n строк и n столбцов называется квадратной матрицей порядка n.
ü Квадратная матрица называется верхнетреугольной (нижнетреугольной), если все её элементы, расположенные ниже (выше) главной диагонали равны нулю.
· Операции над матрицами
Пусть
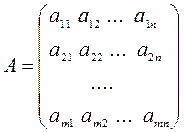 ,
, 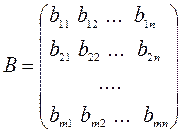
1. Сумма матриц осуществляется поэлементно:
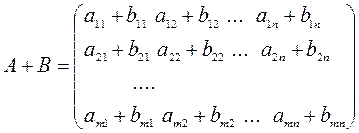 .
.
2. Умножение матрицы на число осуществляется поэлементно:
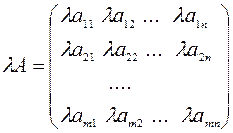 .
.
3. Транспонирование матрицы осуществляется заменой строк столбцами:
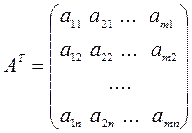 .
.
4. Умножение матрицы строки на матрицу столбец осуществляется по формуле:
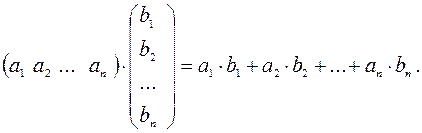
5. Умножение матрицы размера 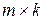 на матрицу размера
на матрицу размера 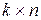 осуществляется последовательным умножением строк первой матрицы на столбцы второй:
осуществляется последовательным умножением строк первой матрицы на столбцы второй:
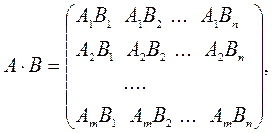
где
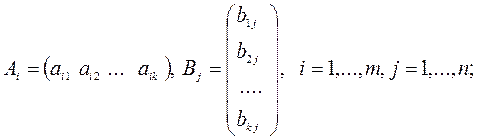
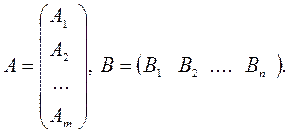
Пример 1.1. Пусть 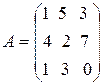 ,
, 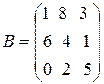 ,
, 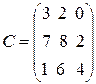 .
.
Найдите матричное выражение АTВ +2A – 3СT.
▼
1. 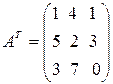 .
.
2. 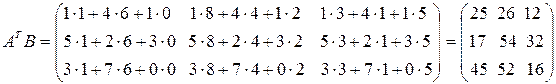 .
.
3. 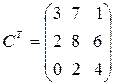 .
.
4. 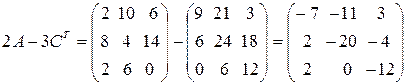 .
.
5. 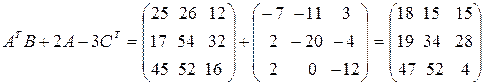 .
.
▲
· Определители
ü Пусть 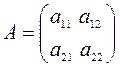 – квадратная матрица второго порядка.
– квадратная матрица второго порядка.
Определителем второго порядка матрицы A называется число:
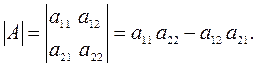
ü Пусть 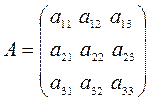 – квадратная матрица третьего порядка.
– квадратная матрица третьего порядка.
Определителем третьего порядка матрицы A называется число:
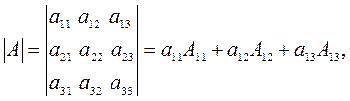
где
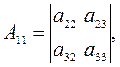
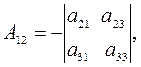
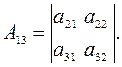
· Пусть 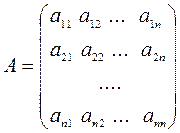 – квадратная матрица n -го порядка.
– квадратная матрица n -го порядка.
Определителем n-го порядка матрицы A называется число:
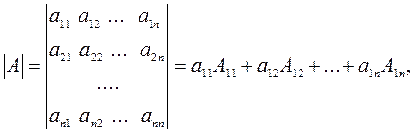
где 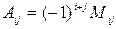 - алгебраическое дополнение элемента
- алгебраическое дополнение элемента 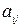 .
.
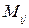 – (минор элемента
– (минор элемента 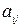 ) определитель порядка n–1 матрицы, полученной из матрицы A, вычёркиванием строки i и столбца j.
) определитель порядка n–1 матрицы, полученной из матрицы A, вычёркиванием строки i и столбца j.
Пример 1.2. Найти определитель матрицы 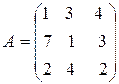 .
.
▼
1.Найдём алгебраические дополнения первой строки:
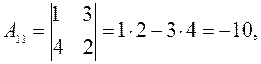
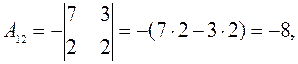
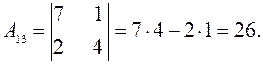
2. Вычисляем определитель 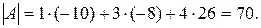
▲
 2015-04-12
2015-04-12 710
710








