2015-04-12
575
Пусть X – случайная величина. Случайную величину X – M(X) называют отклонением. Очевидно, что математическое ожидание отклонения равно 0:
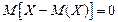(17.1)
Дисперсией (рассеянием) случайной величины называют математическое ожидание квадрата отклонения от ее математического ожидания, т.е.
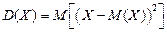(17.2)
Дисперсия характеризует меру рассеяния возможных значений случайной величины по отношению к ее математическому ожиданию.
Нередко вместо формулы (1) в вычислениях используют эквивалентную ей формулу
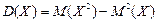(17.3)
Действительно, D (X) = M((X - M(X))2)= M[(X2 - 2X·M(X) + M2(X)]=
= M(X2) - 2 M(X)·M(X) + M[M2(X)] = M(X2) - M2 (X).
Свойства дисперсии:
1. Дисперсия постоянной величины равна нулю, т.е. D(С) =0
2. Постоянный множитель можно выносить за знак дисперсии, возводя его в квадрат, т.е.
D(CX) =C2D(X). (17.4)
3. Дисперсия суммы или разности двух независимых случайных величин равна сумме их дисперсий
D(X ± Y) = D(X) + D(Y). (17.5)
Доказательство.
а) D (X + Y) = M (X ² + 2 XY + Y ²) – (M (X) + M (Y))² = M (X ²) + 2 M (X) M (Y) +
+ M (Y ²) – M ²(X) – 2 M (X) M (Y) – M ²(Y) = (M (X ²) – M ²(X)) + (M (Y ²) – M ²(Y)) = D (X) + D (Y).
|
|
|
б) D (X – Y) = D (X) + D (- Y) = D (X) + (-1)² D (Y) = D (X) + D (X).
Следствие: D(C + X) = D(X), где С – постоянная.
Дисперсия D(X) имеет размерность квадрата единицы размерности случайной величины X. Это создает определенные неудобства, поэтому вводят показатель рассеяния случайной величины, имеющей ту же размерность, что и случайная величина. Для этого извлекают квадратный корень из дисперсии. Полученную величину называют средним квадратическим отклонением (стандартом) и обозначают σ(X)
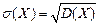, (17.6)
тогда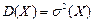 
.
Начальным моментом порядка k случайной величины Х называют математическое ожидание величины Хk:
νk=M(Хk) (17.7)
в частности, ν1=M(Х), ν2=M(Х2)
Пользуясь этими моментами формулу для вычисления дисперсии можно записать так:
D (X) = ν2 - ν12
Центральным моментом порядка k случайной величины Х называют математическое ожидание величины (Х – М(Х))k
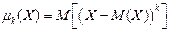(17.8)
В частности, μ1 = M (Х – М (Х)) = 0, μ2 = M ((Х – М (Х))2) = D (X).
Можно получить соотношения, связывающие начальные и центральные моменты:
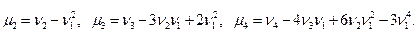(17.9)
