Определение. Минором порядка k матрицы A называется определитель матрицы k-го порядка, элементы которой стоят на пересечении выбранных k – строк и k – столбцов, т.е..
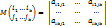
Определение. Минор порядка r матрицы A называется базисным, если он отличен от нуля, а все миноры более высокого порядка равны нулю (если они существуют).
Определение. Рангом матрицы А называется порядок её базисного минора, т.е.. ранг матрицы A равен r, если в матрице существует ненулевой минор r-го порядка, а все миноры более высокого порядка равны нулю (если они существуют). Обозначается Rg A.
Определение. Минор, определяющий ранг матрицы, называется Базисным минором. Строки и столбцы, формирующие базисный минор, называются базисными строками и столбцами.
Теорема о базисном миноре. Столбцы матрицы А, входящие в базисный минор, образуют линейно независимую систему. Любой столбец матрицы А линейно выражается через базисные столбцы.
Доказательство. Amxn = || aij ||mxn Пусть k – порядок базисного минора. Без ограничения общности считаем, что базисный минор расположен в левом верхнем углу.
|
|
|
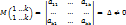
1) Если базисные столбцы линейно зависимы, то столбцы базисного минора так же линейно зависимы => хотя бы один из столбцов линейно выражается через остальные, т.е.. является их линейной комбинацией => Δ = 0, что противоречит условию => базисные столбцы линейно независимы.
2) Зафиксируем произвольный столбец матрицы А, например 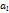 . Покажем, что
. Покажем, что 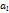 линейно выражается через базисные столбы. Построим определитель
линейно выражается через базисные столбы. Построим определитель

(1≤ l ≤n) (1≤ i ≤m)
Если i < k или l < k, то 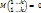
Рассмотрим случай i > k, l > k Тогда 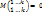 как минор k+1– го порядка в матрице А. Обозначим А1, …, Аk, Ak+1 алгебраические дополнения к последней строке
как минор k+1– го порядка в матрице А. Обозначим А1, …, Аk, Ak+1 алгебраические дополнения к последней строке 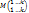 Эти величины не зависят от элементов i-ой строки. Кроме того Ak+1 = Δ ≠ 0. Разложим минор по последней строке. ai1 A1+…+ aik Ak + ail Δ = 0
Эти величины не зависят от элементов i-ой строки. Кроме того Ak+1 = Δ ≠ 0. Разложим минор по последней строке. ai1 A1+…+ aik Ak + ail Δ = 0
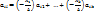 l = 1, …, n ч.т.д.
l = 1, …, n ч.т.д.
Следствие 1. Пусть Аmxn Если Rg A < n, то столбцы матрицы линейно зависимы.
Доказательство. Пусть Rg A = k < n, значит в матрице существует базисный минор порядка k. Не ограничиваясь общности будем считать, что ↓a1, …, ↓ak базисные. Т.к.. k < n, то ∃ ↓ak+1. По теореме о базисном миноре столбец ↓ak+1 выражается через базисные, т.е.. ↓a1, …, ↓ak, ↓ak+1 – линейно зависимы => матрица содержит линейно зависимую подсистему => матрица линейно зависима.
Следствие 2. Пусть А – квадратная матрица. det A = 0 óстолбцы матрицы линейно зависимы.
Доказательство. Если столбцы линейно зависимы, то det A = 0. Пусть det A = 0, тогда Rg A < n, т.е.. число столбцов больше ранга => (из следствия 1) столбцы матрицы линейно зависимы.
 2015-04-12
2015-04-12 12253
12253







