Билет 4. Критерий совместимости систем ЛАУ (теорема Кронкеля – Капелли)

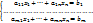
(1) Система ЛАУ из m уравнений с n неизвестными; = (A|b_↓) = (_↓a₁ … _↓a_n | b_↓) – расширенная матричная система (1); Ax_↓ = b_↓ ó _↓a₁x₁+…+_↓a_nx_n = b_↓ (1’)

Определение. Система ЛАУ называется совместной, если она имеет хотя бы одно решение.

Теорема Кронкеля – Капелли. Система ЛАУ совместна в том и только в том случае, когда ранг матрицы системы равен рангу расширенной матрицы системы, т.е.. Rg A = Rg

Доказательство. Необходимость. Пусть система совместна => существуют решения (α₁… α_n)^T. Подставим их в (1’): _↓a₁ α₁+…+_↓a_n α_n = b_↓; Rg = Rg(_↓a₁ … _↓a_n | b_↓) = Rg(_↓a₁ … _↓a_n | b_{↓ — ↓}a₁ α₁-…-_↓a_n α_n) = Rg(_↓a₁ … _↓a_n | 0_↓) = Rg(A|0_↓) = Rg A

Достаточность. Пусть Rg A = Rg => базисный минор матрицы А является базисным минором матрицы => столбец b_↓ линейно выражается через базисные столбцы матрицы А, т.е.. ∃ (α₁… α_n) такие, что b_↓ = _↓a₁ α ₁+…+_↓a_n α _n => (α ₁… α _n)^T – решение системы (1). ч.т.д.