V – линейное пространство  и
и  - линейное подпространство пространства V.
- линейное подпространство пространства V.
Определение 9: Пересечением 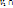
 линейных подпространств
линейных подпространств  и
и 
называется множество всех элементов, которые принадлежат этим подпространствам одновременно: 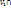
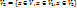
Суммой  +
+  линейных подпространств
линейных подпространств  и
и  называется множество всех элементов пространства V вида
называется множество всех элементов пространства V вида 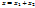 , где
, где 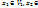
 .
.
 +
+ 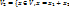 ,
, 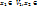

Теорема 10: Сумма и пересечение линейных подпространств являются сами подпространствами.
Доказательство: 1) Рассмотрим сумму
 +
+ 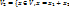 ,
, 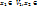

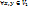 +
+  λ
λ 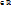 :
: 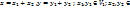

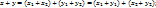
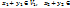
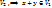 +
+ 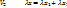
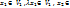

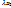

 =>
=>  +
+  - линейное подпространство.
- линейное подпространство.
2) Рассмотрим пересечение 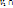
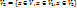
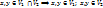 ;
; 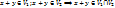
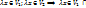


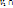
 - линейное подпространство.
- линейное подпространство.
Определение: Сумма  +
+  называется прямой суммой, если
называется прямой суммой, если 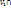
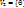 .
.
Обозначение: 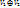 - прямая сумма подпространств
- прямая сумма подпространств  и
и  .
.
Теорема: Каждый элемент 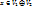 представляется в виде
представляется в виде 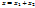 , где
, где 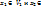
 единственным способом.
единственным способом.
Доказательство: Пусть 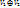 прямая сумма
прямая сумма 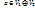 , и
, и 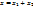 ,
, 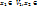

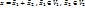 ,
, 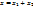 =
= 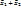
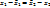
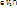
 = {
= {  }
} 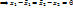 , т.е.
, т.е.  =
=  и
и  =
= 
Теорема: Линейное (конечномерное) пространство V является прямой суммой подпространств  и
и  (т.е.V =
(т.е.V = 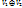 ) тогда и только тогда, когда:
) тогда и только тогда, когда:
1) dim V=dim  +dim
+dim  и 2)
и 2) 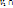
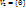 (без доказательства)
(без доказательства)
 2015-04-12
2015-04-12 1654
1654
