Действия с линейными операторами и их свойствами

Определение 1: Оператором (преобразованием) линейного пространства V называется закон, по которому каждому элементу пространства V ставится в соответствие единственный элемент того же самого пространства.

Пусть А – оператор пространства 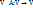. 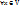обозначим A x – результат действия A на x.

Если 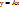, где 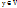, то y называется образом элемента 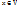, а x – прообразом элемента .

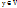Определение 2: Оператор А линейного пространства V называется линейным оператором, если 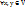и ∀λ 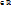выполняются условия:

1) А(x+y)=Ax+Ay

2) A(λx)= λ(Ax)

Простейшие свойства:

Пусть 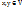, а λ - число. А – линейный оператор.

1) Линейный оператор отображает нулевой элемент на нулевой элемент, т.е.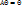

Доказательство::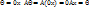

2)

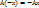
Доказательство: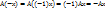

3) Оператор А линейного пространства V является линейным оператором тогда и только тогда, когда 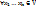и 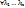выполняется:

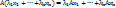
4) Если 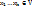линейно зависимы, а А – линейный оператор V, то образы 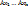- так же линейно зависимы.

Доказательство: т.к. 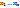- линейно зависимы, то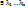

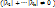, что.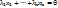

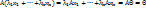
- линейно зависимы.

Определение 3: 1) Пусть А и В – операторы линейного пространства V.

Операторы А и В называются равными (А=В), если .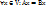

2) Оператор J называется тождественным (или единичным),

если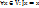

3) Оператор О называется нулевым, если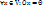

J и O – линейные операторы V.

Примеры:

1) 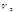- линейное пространство геометрических векторов на плоскости.

а) 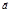- фиксированный.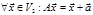

,

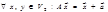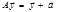
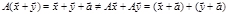=> оператор не линейный

б) Все векторы 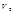: Приложим к фиксированной точке О. φ – фиксированный угол.

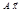- вектор, полученный поворотом 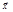вокруг О на угол φ.

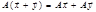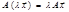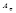; ; => - линейный оператор.

2) 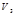- линейное пространство геометрических векторов в пространстве, приложенных к началу координат.

А – оператор проектирования вектора 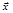на плоскость ХОУ

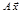- проекция вектора 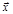на ХОУ

А – линейный оператор.

3) 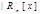- линейное пространство множителей степени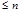

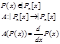
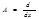=> - оператор дифференцирования.

Действия над линейными операторами:

V – линейное пространство.

L(V) – множество линейных операторов линейного пространства V

Определение 4: Суммой операторов А+В называется оператор А+В, который действует по правилу: :.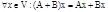

Произведением оператора А на число λ называется оператор λА, действующий по правилу: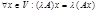

Свойства произведения операторов:

1) λ(АВ)=(λА)В=А(λВ)

2) (А+В)С=АС+ВС

3) А(В+С)=АВ+АС

4) (АВ)С=А(ВС)

5) AJ=JA=A

6) AO=OA=O