В других случаях, когда кривая ℒ задана:
а) явно: y = f(x), 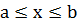
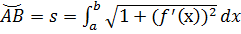
б) параметрически: 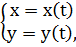
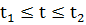 :
: 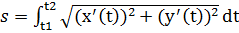
в) в полярных координатах
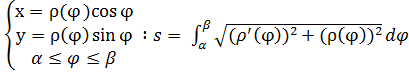 .
.
| M |
| A |
| r(t) |
Ранее получили, что 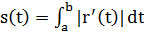 – длина дуги кривой.
– длина дуги кривой. 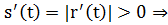 поэтому введенная функция монотонно-возрастающая и её можно взять в качестве параметра, задающего уравнения кривой линии. Действительно
поэтому введенная функция монотонно-возрастающая и её можно взять в качестве параметра, задающего уравнения кривой линии. Действительно 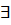 обратная к
обратная к 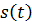 функция (в силу монотонности), т.е. t = t(s) и тогда
функция (в силу монотонности), т.е. t = t(s) и тогда 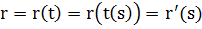 . Такая параметризация кривой называется натуральной или естественной.
. Такая параметризация кривой называется натуральной или естественной.
Замечание. В отличии от обычной параметризации производную радиус-функции в естественной параметризации будем обозначать 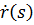
Её важное свойство: 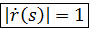 .
.
□ Из формулы длины дуги получим: 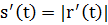 , тогда
, тогда
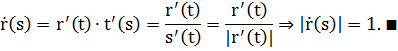
 2015-04-12
2015-04-12 719
719








