Радиус и центр кривизны кривой

На предыдущей лекции мы выяснили, что радиус и центр соприкасающейся окружности (или окружности кривизны) и является радиусом и центром кривизны кривой. Выясним их математический смысл.

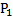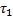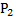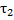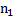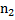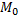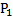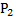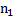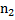M

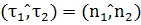
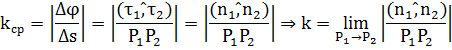
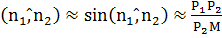, тогда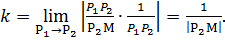

Отрезок 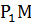называют радиусом кривизны, 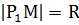. Получили, что .

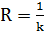Def (центр кривизны). Точку М₀ как точку пересечения 2-х нормалей кривой выходящих из точек 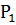и 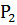при стремлении 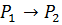называют центром кривизны кривой центр кривизны кривой находят на нормали кривой проведенной в данной т. 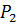на расстоянии обратном к кривизне кривой в этой точке .

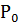Выводим формулы для координат центра кривизны:

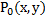R

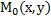1) центр кривизны принадлежит нормали кривой построенной в т. 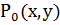, т.е.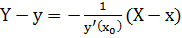

2) центр кривизны является центром соприкасающейся окружности, т.е.

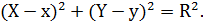
Решаем совм-ю систему:

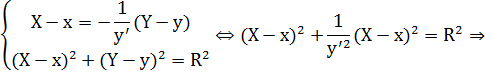
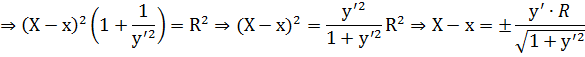
и .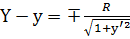

Получим следующие координаты центра кривизны: (учитывая, что 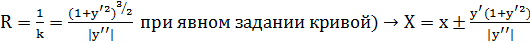и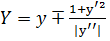

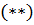
Для выяснения знака надо рассмотреть случаи, когда 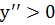и 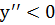. Если 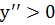, то кривая выпукла вниз. Следовательно, 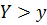и надо взять нижние знаки.

Замечание. Если кривая задана параметрическими уравнениями: х = х(t), y = y(t), то подставим в формулу (**) значения 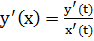и 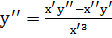получаем 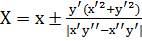и .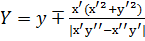

Определения. 1) Множество всех центров кривизны данной линии называется эволютой.

2) По отношению к своей эволюте исходная линия называется эвольвентой (или разверткой)

Пример: 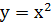. Найти её эволюту.

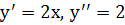
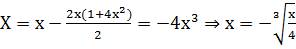
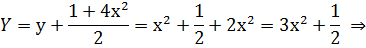
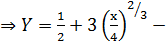уравнение эволюты