Кривизна кривой

M

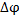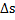P

O

Одной из основных числовых характеристик кривой является кривизна, показывающая на сколько кривая отклоняется от прямой линии.

Рассмотрим угол между касательными в т. Р(r(t)) и в т. М(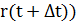 - угол смежности 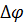. (Если касательная поворачивается против часовой стрелки, то угол смежности положительный, а по часовой стрелке - отрицательный).

Средней кривизной в т. Р считаем: 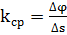и .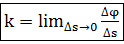

Формулы кривизны

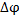P

A

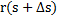r(s)

M

B

P=M

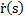H

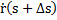A

B

Учитывая, что при общей параметризации s = s(t), 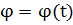, получаем .

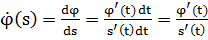Вернемся к натуральной параметризации кривой

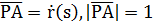
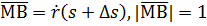
Соединим 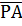и 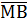в одну точку. 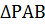- равнобедренный. Проведем биссектрису РН.

Получаем:

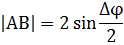
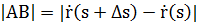
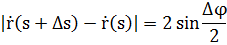
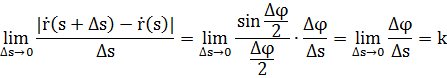
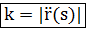
Замечание. Т.к. 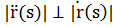, то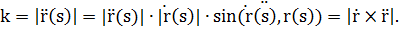

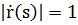
Для кривой в общей параметризации: r = r(t).

Пересчитаем производные: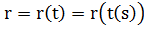

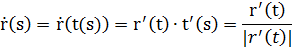
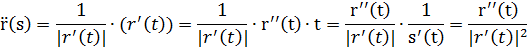
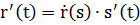
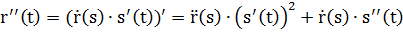
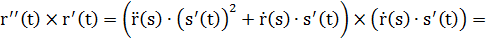
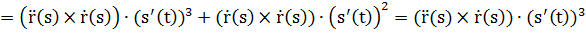
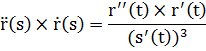
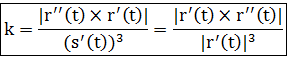
Различные формулы кривизны плоской кривой.

В координатах: r(s) = (x(s), y(s))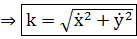

Векторно-параметрический способ задания кривой: 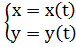, 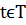. Тогда .

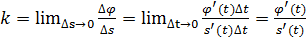Теорема. Дважды непрерывно дифференцируемая кривая без особых точек имеет в каждой точке определенную кривизну k.

Эта кривизна определяется по формуле: 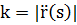в естественной параметризации кривой или 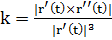(*) в общей параметризации кривой.

В частности для плоской кривой:

а) если кривая задана параметрически: ,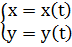

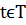
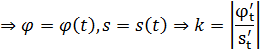
Получим формулу вычисления кривизны кривой из уравнения (*) для трехмерного случая:

,

(*)

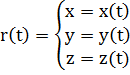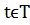
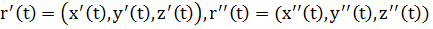
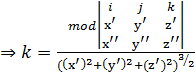
Тогда в двухмерном случае будет:

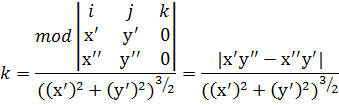
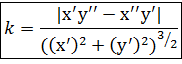
б) кривая задана явно: y = f(x). Перейдем к параметрическому способу задания: х = t, y = f(t)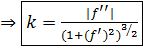

в) кривая задана неявно: F(x,y) =0, у = у(х), F(х, у(х))=0

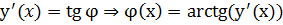
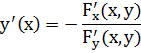
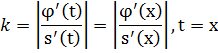
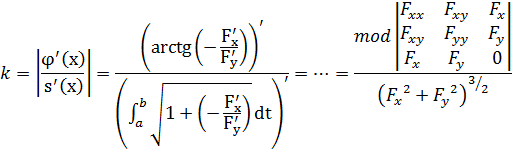
г) кривая задана в полярных координатах:

,

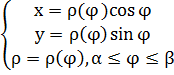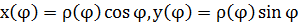
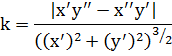
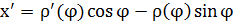
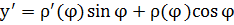
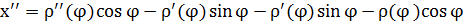
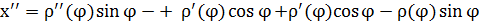
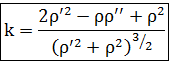
Вектор кривизны. Вектор ,будем называть вектором кривизны. Его длина ,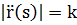

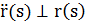
Единичный вектор 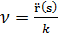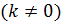– называется главной нормалью ().

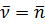Знак кривизны. Кривизна по определению неотрицательна. Для плоских кривых можно определить знак.

Радиус кривизны кривой. Центр кривизны кривой. Круг кривизны кривой (для плоской кривой)

Рассмотрим плоскую кривую ℒ с кривизной 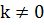. В малой окрестности точки 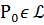кривую можно заменить ее касательной прямой в этой точке. Это первое приближение. Второе приближение кривой является соприкасающаяся окружность (вернее её малая дуга).

Расположим оси координат так, что начало координат совпадет с т. 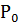и ось Ох казалась кривой ℒ в этой точке. Пусть у = у(х) – уравнение кривой, а 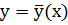- уравнение окружности проходящей через т. .

Def. Окружность 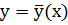называется соприкасающейся, если в т. х = 0 совпадают между собой значения функции у(х) и и их первых и вторых производных, т. е. 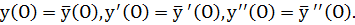(функции 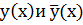совпадают с точкой О()).

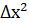Следствие: 1)Касательные совпадают в т.

2) Кривизны совпадают в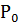

Def. Радиус окружности 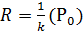- и называется радиусом кривизны кривой ℒ в т. 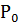. Центр соприкасающейся окружности………….