2015-04-12
2138
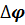
Q M ℒ
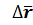
Р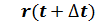 
R(t)
Def (касательной). Прямая PQ к которой стремится секущая PH при H – P (по кривой) называется касательной к кривой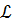 
в точке Р.
Теорема. Гладкая кривая (n=1)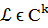 
без особых точек имеет в любой точке Р касательную.
Замечание. Покажем, что вектор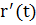 
(вычисляемый в точке Р) является направляющим вектором …. к кривой (
).
: 
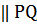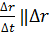и при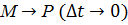 
, т. е. в силу дифференцируемости r(t) в т. Р (
) 
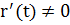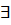… предел 
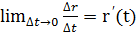и с другой стороны секущая при 
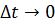переходит в касательную. 
Тогда (из аналитической геометрии) уравнения касательной к кривой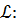 
а) в векторно-параметрической форме: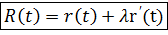 
, 
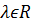– параметр
б) в параметрической форме: (т.к.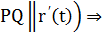 
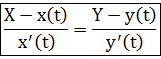
или
.
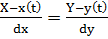в) кривая заданная явным уравнением: y = f(x). Параметризуя это уравнение: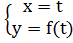 
и используя предыдущую формулу, получаем: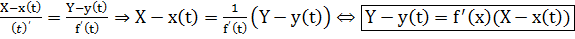 
г) кривая задана неявным уравнением: F(x,y) =0. Из математического анализа: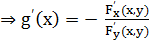 
и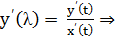 
подстав. в …
.
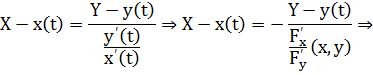
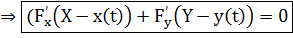Нормаль к кривой
 |
| P |
| O |
| R |
| N |
| P |
| |
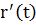| r(t) |
| O |
| N |
Теорема сохраняется (см. выше)
а) в параметрической форме: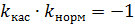 
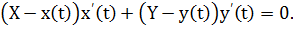
б) в векторно-параметрической форме: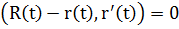 
в) явное задание кривой: из касательной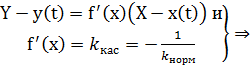 
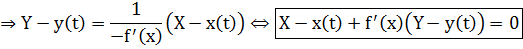
г) неявное задание кривой:
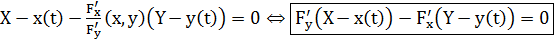или
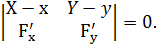
Таблица
| Способ задания | Уравнение касательной | Уравнение нормали |
| Параметрический: х = х(t) y = y(t) |  |  |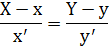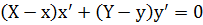
| Явный: y = f(x) |  |  |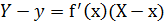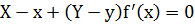
| Неявный: F(x,y) =0 |  |  |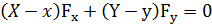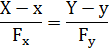
Пример. Составить уравнение касательной и нормали к линии:
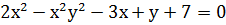в т. (1; 2)
