Первая квадратичная форма поверхности (метрика поверхности)

Def. Первой квадратичной формой поверхности Ф называется квадрат полного дифференциала 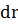вектор-функции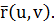

Линейный элемент

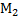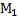y

y+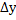

(x,y)

x+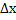

x

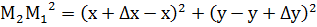
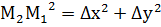
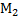y

Аффинная система координат:

x

O

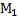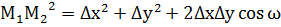
Рассмотрим регулярную поверхность.

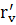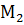v

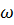
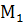Q

u

r = r(u,v)

Найти расстояние 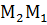для криволинейного .

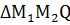При 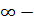малом смещении т. криволинейный треугольник можно рассматривать как прямолинейный (длина дуги хорде стягивающей эту дугу).

Тогда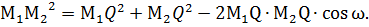

Если поверхность задана векторной параметризацией: r = r(u,v), то

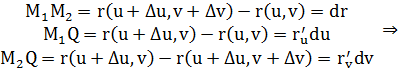
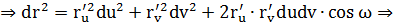
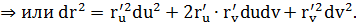
Учитывая, что 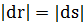и введя обозначения 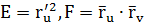и 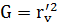получим:

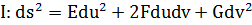(1)

Замечание 1. Выражение в 1-й части уравнения (1) называют: первая основная гауссовская квадратичная дифференциальная форма.

Замечание 2. Первая квадратичная форма представляет двумерный вариант метрики поверхности. Метрика не определяет однозначно форму поверхности.

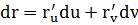
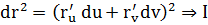
Приложения 1-й квадратичной формы.

Форма дает возможности: 1) вычислить расстояние или длины дуг на поверхности;

2) вычислить углы между линиями на поверхности;

3) вычислить площадь фигур на поверхности.

Геометрический смысл коэффициентов 1-й квадратичной формы.

Q

M

u

Q1

v

1) 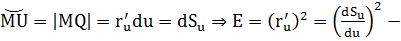квадрат производной дуги координатной линии и по её же параметру.

2) Аналогично .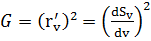

3)

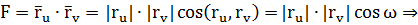
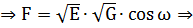знак F зависит от .

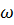Замечание. 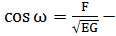угол между координатными линиями на поверхности.