Кривизна характеризует отклонение кривой от криволинейной формы, а кручение (2-я кривизна) – отклонение кривой от плоской формы
| b |
| b |
| ψ |
| P0 |
| M |
Пусть т. 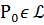 и М – т. близкая к т.
и М – т. близкая к т. 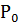 . Обозначим
. Обозначим 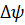 - угол между соприкасающимися плоскостями в этих точках (или угол между бинормалями).
- угол между соприкасающимися плоскостями в этих точках (или угол между бинормалями).
Тогда под абсолютным кручением кривой 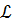 в т.
в т. 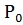 будем понимать:
будем понимать: 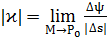
Кручение
Теорема. Регулярная (трижды непрерывно дифференцируемая) кривая в каждой своей точке, где кривизна отлична от нуля, имеет определение абсолютное кручение 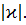 Если
Если 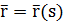 естественная параметризация кривой, то
естественная параметризация кривой, то
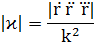
□ Если кривизна в т. 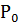 отлична от нуля, то она отлична от нуля в окрестности т.
отлична от нуля, то она отлична от нуля в окрестности т. 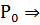 вектора
вектора 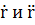 - не коллинеарны
- не коллинеарны 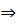 в любой т. М близкой к
в любой т. М близкой к 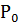 существует единственная соприкасающаяся плоскость
существует единственная соприкасающаяся плоскость
b(s+ 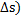 |
| b(s) |
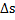 |
| P0 |
| M |
b(s+ 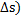 |
| b(s) |
 ψ ψ |
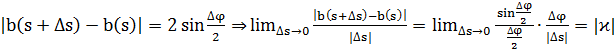
b(s+ 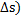 |
| b(s) |
 ψ ψ |
| n |
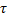 |
 |
Получим, что 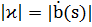 .
.
Но 1) 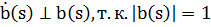 (свойство векторной функции).
(свойство векторной функции).
2) 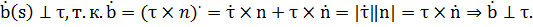
Из 1) и 2) следует, что 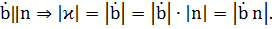
Известно, что 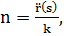
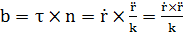 , тогда
, тогда 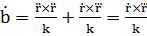 .
.
Получаем: 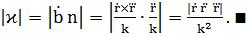
О знаке кручения (определение кручения)
Из параллельности векторов 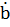 и
и 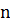 следует, что при движении по кривой в сторону возрастающих s соприкасающаяся плоскость кривой поворачивается около касательной (кручение, длина вектора
следует, что при движении по кривой в сторону возрастающих s соприкасающаяся плоскость кривой поворачивается около касательной (кручение, длина вектора 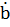 выражает скорость вращения вектора бинормали, а следовательно соприкасающейся плоскости).
выражает скорость вращения вектора бинормали, а следовательно соприкасающейся плоскости).
Кручение кривой определяется равенством 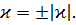 Знак «+» берется, если вращение соприкасающейся плоскости происходит в направлении от b к
Знак «+» берется, если вращение соприкасающейся плоскости происходит в направлении от b к 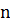 и «
и «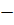 », если вращение происходит в направлении от
», если вращение происходит в направлении от 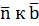 . Таким образом,
. Таким образом, 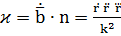 .
.
Замечание. Точки кривой, в которых кручение равно нулю, называются точками уплощения.
Вычисление кручения
1) Кривая r = r(t) задана в естественной параметризации.
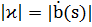 ,
, 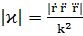
1) Так как 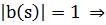
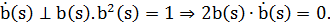
2) 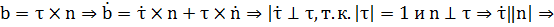
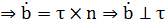
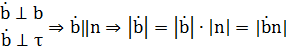
Но 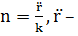 вектор кривизны.
вектор кривизны.
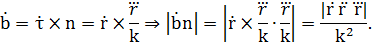
О знаке. Т.к. 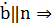 при движении вдоль кривой в сторону возрастания параметра s соприкасающаяся плоскость поворачивается возле касательной. Если движение происходит от от b к
при движении вдоль кривой в сторону возрастания параметра s соприкасающаяся плоскость поворачивается возле касательной. Если движение происходит от от b к 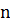 , то «+» и если от
, то «+» и если от 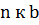 , то «
, то «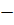 ».
».
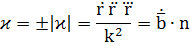
2) Кривая r = r(t) задана векторно-параметрически:
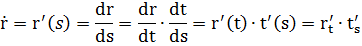
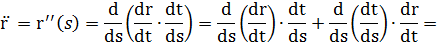
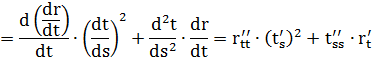
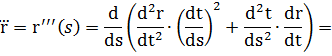
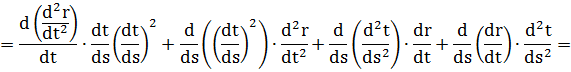
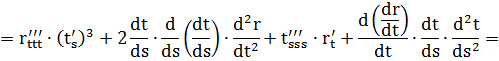
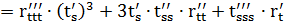
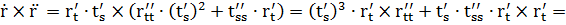
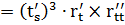
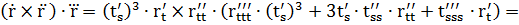
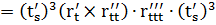
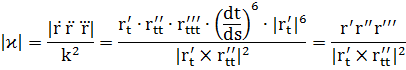
3) Кривая задана параметрически: 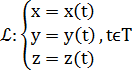
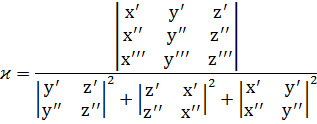
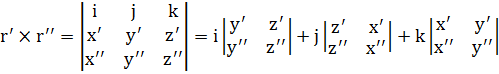
4) Кривая задана явно: 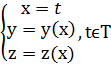
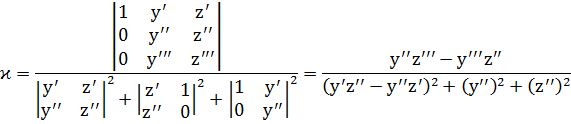
 2015-04-12
2015-04-12 2488
2488








