1) Понятие поверхности. Определение поверхности.
Def. Под элементарной поверхностью (простой поверхностью) понимают любые семейства точек, которые можно топологично отобразить на замкнутый круг.
Замечание. Локально (в малом) поверхность получается в результате непрерывной деформации в 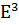 (гомоморфизм) плоской области.
(гомоморфизм) плоской области.
Глобально (в целом) поверхность «склеивается» из таких кусков.
Def. Поверхностью называют множество точек, состоящих из конечного или счетного множества простых поверхностей склеенных друг с другом.
Будем рассматривать поверхности, которые гомоморфны некоторой плоской области D. Область D – область плоскости переменных u и v.
Замечание. Гомоморфизм же области D в пространстве 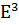 , в результате которого и возникает рассматриваемая поверхность, обычно задают, выбрав
, в результате которого и возникает рассматриваемая поверхность, обычно задают, выбрав 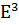 … - т. О и вектор-функцию
… - т. О и вектор-функцию 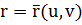 .
.
2) Способы задания поверхности:
| O |
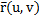 |
а) векторно-параметрический: r = r(u,v).
б) если в 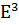 введена прямоугольная система координат:
введена прямоугольная система координат:
r(u,v) = х(u,v)i + y(u,v)j + z(u,v)k
в) в частном случае, когда из уравнений 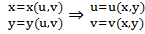 и подставим в
и подставим в 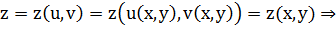 явное уравнение поверхности
явное уравнение поверхности 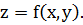
г) неявное задание поверхности: 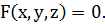
Замечание. Мы будем изучать регулярные или дифференцируемые поверхности.
Def. Поверхность является 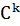 - гладкой (регулярной) поверхностью, если среди её параметризации найдется такая параметризация r = r(u,v), что вектор-функция r(u,v) – n раз непрерывно диффенцируема и в каждой точке (u,v) её первые частные производные
- гладкой (регулярной) поверхностью, если среди её параметризации найдется такая параметризация r = r(u,v), что вектор-функция r(u,v) – n раз непрерывно диффенцируема и в каждой точке (u,v) её первые частные производные 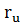 (u,v) и
(u,v) и 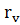 (u,v) неколлинеарны.
(u,v) неколлинеарны.
3) Кривые на поверхности. Координатные линии.
Рассмотрим в пространстве поверхность Ф заданную гладкой параметризацией r = r(u,v). Вектор-функция r(u,v) определена в области D переменных u и v.
Если в области D выбрать кривую 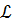 , то её образом будет кривая
, то её образом будет кривая 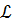 на поверхности Ф. Кривую
на поверхности Ф. Кривую 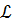 в D можно задать параметрически:
в D можно задать параметрически: 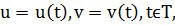 тогда
тогда 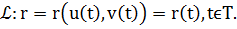
Замечание 1. Уравнения 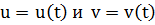 называются внутренними уравнениями кривой
называются внутренними уравнениями кривой 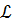 на поверхности Ф.
на поверхности Ф.
Замечание 2. Если в качестве внутренних уравнений взять семейства кривых:
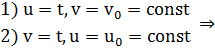
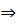 координатная сеть на множестве D, то они определяют координатные линии на поверхности Ф.
координатная сеть на множестве D, то они определяют координатные линии на поверхности Ф.
4) Касательная плоскость к поверхности Ф.
Def. Под касательной плоскостью к любой поверхности в данной точке будем понимать плоскость, которая содержит все касательные прямые к кривым, лежащим на поверхности и проходящим через выбранную точку. Это определение подтверждает следующее:
Теорема. Пусть Ф – гладкая поверхность, вектор-функция r(u,v) определенная на D её гладкая параметризация. Точка 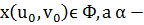 плоскость, проходящая через т. х и имеющие векторы
плоскость, проходящая через т. х и имеющие векторы 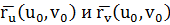 своими направляющими векторами. Тогда все касательные прямые в т. х к гладким кривым, лежащим на поверхности Ф и проходящим через т. х, содержаться в плоскости
своими направляющими векторами. Тогда все касательные прямые в т. х к гладким кривым, лежащим на поверхности Ф и проходящим через т. х, содержаться в плоскости 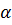 и заполняют
и заполняют 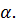
Из теоремы следует, что векторы R – r, 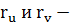 компланарные
компланарные 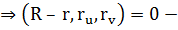 векторное уравнение касательной плоскости или через координаты:
векторное уравнение касательной плоскости или через координаты:
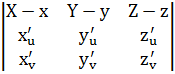 =0.
=0.
В случае явного задания поверхности: 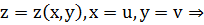
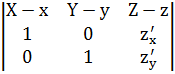 =0 или
=0 или 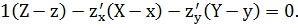
В случае неявного задания поверхности:
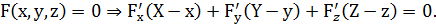
5 ) Нормаль к поверхности и её уравнение.
Определение. Прямая, проведенная через заданную точку поверхности и ортогональная касательной плоскости поверхности проведенной через эту же точку поверхности, называется нормалью к поверхности в данной точке.
Замечание. Иногда называют вектор  касательной плоскости в данной точке.
касательной плоскости в данной точке.
Уравнение нормали: 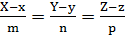 , где
, где 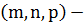 координаты вектора
координаты вектора
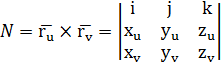
В этом случае: а) для явного задания поверхности:
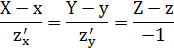
б) для неявного:
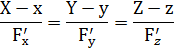
 2015-04-12
2015-04-12 1706
1706








