2015-04-17
308
Гипотеза о статистической значимости коэффициентов регрессии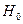 
: 
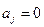, j = 1, 2, …, m, при альтернативной гипотезе : 
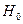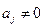проверяется с помощью t- статистики, которая определяется как отношение величины оценки коэффициента 
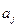к его стандартной ошибке 
: 
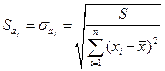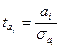, имеющей распределение Стьюдента с 
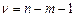числом степеней свободы. Величина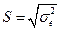 
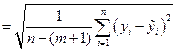называется стандартной ошибкой регрессии.
По выборочным данным вычисляется наблюдаемое значение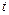 
-статистики t набл, по таблицам критических точек распределения Стьюдента находятся критические значения 
= 
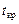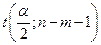. Если 
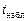попадает в критическую область, т.е.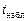 
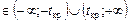, то нулевая гипотеза 
: 
, 
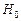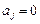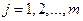, отвергается и коэффициент 
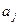значимо отличается от нуля. В противном случае, считается, что фактор 
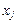линейно не связан с зависимой переменной, и его рекомендуется исключить из уравнения регрессии.
Доверительные интервалы для каждого коэффициента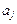 
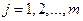, , регрессии имеют вид 
.
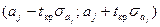Если незначимым окажется коэффициент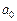 
, проводится пересчет уравнения регрессии в предположении, что 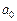= 0.
