Операция предельного перехода является одной из основных в математическом анализе.
Определение 1. Число 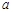 называется пределом последовательности
называется пределом последовательности  , если для любого положительного действительного числа
, если для любого положительного действительного числа 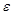 найдется такой номер
найдется такой номер 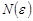 , что при всех
, что при всех 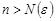 элементы этой последовательности удовлетворяют неравенству
элементы этой последовательности удовлетворяют неравенству 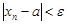 .
.
Символическая запись:
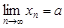
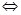
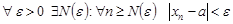 .
.
Последовательности, имеющие предел 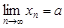 ,
, 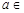
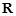 , называются сходящимися (к числу а), а последовательности, не имеющие конечного предела, – расходящимися.
, называются сходящимися (к числу а), а последовательности, не имеющие конечного предела, – расходящимися.
2. Неравенство 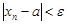 означает, что последовательность
означает, что последовательность 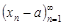 является бесконечно малой последовательностью. Отсюда следует, что любую сходящуюся последовательность можно представить в виде
является бесконечно малой последовательностью. Отсюда следует, что любую сходящуюся последовательность можно представить в виде 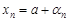 , где
, где 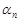 – бесконечно малая последовательность. Очевидно, что
– бесконечно малая последовательность. Очевидно, что
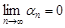
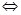
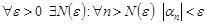 .
.
3. Бесконечно большая последовательность  имеет бесконечный предел:
имеет бесконечный предел:
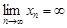
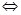
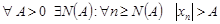 .
.
 2015-04-17
2015-04-17 547
547








