Определение 1. Последовательность  называется неубывающей, если ее элементы удовлетворяют условию
называется неубывающей, если ее элементы удовлетворяют условию 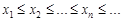 .
.
Последовательность  называется возрастающей, если ее элементы удовлетворяют условию
называется возрастающей, если ее элементы удовлетворяют условию 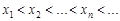 .
.
Последовательность  называется невозрастающей, если ее элементы удовлетворяют условию
называется невозрастающей, если ее элементы удовлетворяют условию 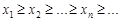 .
.
Последовательность  называется убывающей, если ее элементы удовлетворяют условию
называется убывающей, если ее элементы удовлетворяют условию
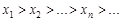 .
.
Определение 2. Последовательность  называется монотонной, если удовлетворяет неравенствам определения 1. Последовательность
называется монотонной, если удовлетворяет неравенствам определения 1. Последовательность  называется строго монотонной, если она возрастающая или убывающая.
называется строго монотонной, если она возрастающая или убывающая.
Очевидно, что монотонные последовательности ограничены, по крайней мере, с одной стороны: неубывающие снизу, невозрастающие сверху.
Терема 1 (Вейерштрасса). Каждая ограниченная монотонная последовательность сходится.
► Пусть последовательность  неубывающая, т.е.
неубывающая, т.е. 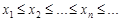 ..
..
Поскольку  ограничена, то
ограничена, то 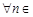
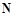
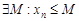 .
.
Рассмотрим множество 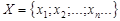 значений последовательности
значений последовательности  . В силу условия, оно не пусто и ограничено. Тогда это множество имеет точную верхнюю грань
. В силу условия, оно не пусто и ограничено. Тогда это множество имеет точную верхнюю грань 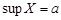 . Согласно определению верхней грани
. Согласно определению верхней грани
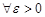
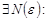
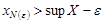 , т.е.
, т.е. 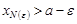 .
.
С другой стороны, по определению верхней грани 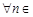
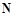 выполняется неравенство
выполняется неравенство 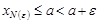 .
.
Тогда 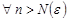 получим
получим 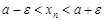 . Отсюда
. Отсюда 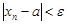 , что означает
, что означает 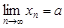 .
.
Аналогично теорема доказывается в случае, когда последовательность невозрастающая. ◄
Замечание. Обратное верно не всегда: не всякая сходящаяся последовательность является монотонной.
 2015-04-17
2015-04-17 443
443








