Пусть задана последовательность  .
.
Определение 6. Последовательность  называется ограниченной сверху (снизу), если существует число
называется ограниченной сверху (снизу), если существует число 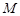 (
(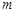 ) такое, что каждый элемент последовательности
) такое, что каждый элемент последовательности 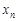 удовлетворяет неравенству
удовлетворяет неравенству 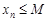 (
(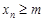 ). Числа
). Числа 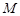 и
и 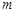 называются верхней и нижней гранями числовой последовательности
называются верхней и нижней гранями числовой последовательности  .
.
Символическая запись:
 – ограничена сверху
– ограничена сверху 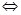
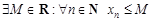 .
.
 – ограничена снизу
– ограничена снизу 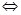
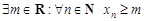 .
.
Определение 7. Последовательность  называется ограниченной, если она ограничена сверху и снизу, т.е. существуют числа
называется ограниченной, если она ограничена сверху и снизу, т.е. существуют числа 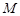 и
и 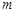 такие, что каждый элемент
такие, что каждый элемент 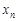 последовательности удовлетворяет неравенству
последовательности удовлетворяет неравенству 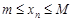 .
.
Символическая запись:
 – ограничена
– ограничена 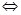
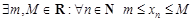 .
.
Пусть 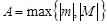 . Тогда условие ограниченности можно записать в виде
. Тогда условие ограниченности можно записать в виде 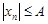 .
.
Определение 8. Последовательность  называется ограниченной, если существует действительное число
называется ограниченной, если существует действительное число 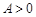 такое, что каждый элемент последовательности
такое, что каждый элемент последовательности 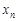 удовлетворяет неравенству
удовлетворяет неравенству 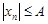 .
.
Определение 9. Последовательность  называется неограниченной, если для любого действительного числа
называется неограниченной, если для любого действительного числа 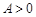 существует элемент
существует элемент 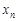 последовательности, удовлетворяющий неравенству
последовательности, удовлетворяющий неравенству 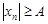 , т.е. либо
, т.е. либо 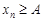 , либо
, либо 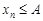 .
.
Символическая запись:
 – неограниченна
– неограниченна 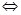
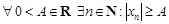 .
.
Пример. Последовательность 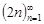 является неограниченной, так как для любого положительного числа
является неограниченной, так как для любого положительного числа 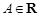
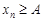 при
при 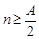 .
.
 2015-04-17
2015-04-17 492
492







