Лемма 1. Если все элементы бесконечно малой последовательности 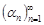 равны одному и тому же числу
равны одному и тому же числу 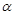 , то
, то 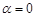 .
.
► Доказываем методом от противного. Предположим, что 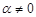 . По определению бесконечно малой последовательности
. По определению бесконечно малой последовательности
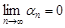
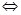
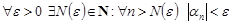 .
.
В силу произвольности 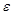 положим
положим 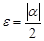 . Тогда
. Тогда 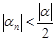 .По условию
.По условию 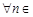
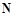
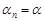 . Подставим в неравенство:
. Подставим в неравенство: 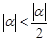 . Отсюда при
. Отсюда при 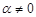 получим
получим 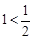 . ◄
. ◄
Теорема 1. Сходящаяся последовательность  имеет только один предел.
имеет только один предел.
► Пусть 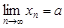 . Доказываем методом от противного. Предположим, что существует еще один предел
. Доказываем методом от противного. Предположим, что существует еще один предел 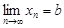 , причем
, причем 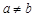 . Из определения предела имеем
. Из определения предела имеем 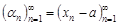 и
и 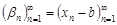 бесконечно малые последовательности. Отсюда
бесконечно малые последовательности. Отсюда 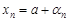 и
и 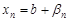 . Приравнивая, получим
. Приравнивая, получим 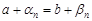 . Тогда все члены бесконечно малой последовательности
. Тогда все члены бесконечно малой последовательности 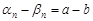 равны одному и тому же числу. По лемме 1 получим
равны одному и тому же числу. По лемме 1 получим 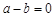 . Значит,
. Значит, 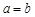 . ◄
. ◄
Теорема 2. Если последовательность  сходится, то она ограничена:
сходится, то она ограничена:
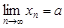
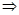
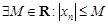 .
.
► Пусть  – сходящаяся последовательность. По определению предела для любого
– сходящаяся последовательность. По определению предела для любого 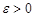 существует натуральное число
существует натуральное число 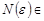
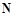 , такое, что для любого
, такое, что для любого 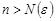 выполняется неравенство
выполняется неравенство 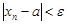 . Тогда для любого
. Тогда для любого 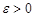 имеет место неравенство:
имеет место неравенство:
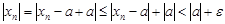 , т.е.
, т.е. 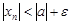 .
.
Пусть 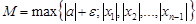 . Тогда
. Тогда 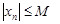
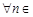
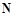 , что и означает ограниченность числовой последовательности. ◄
, что и означает ограниченность числовой последовательности. ◄
Замечание. Обратное верно не всегда: ограниченная последовательность может и не иметь предела.
Теорема 3. Сумма (разность) двух сходящихся последовательностей есть сходящаяся последовательность, предел которой равен сумме пределов последовательностей:
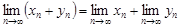 .
.
► Поскольку 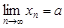 , то можно записать
, то можно записать 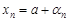 . Аналогично,
. Аналогично, 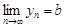 , то
, то 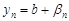 . Здесь
. Здесь 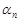 и
и 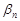 бесконечно малые последовательности при
бесконечно малые последовательности при 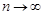 . Тогда
. Тогда
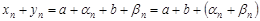 .
.
Последовательность 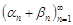 есть бесконечно малая последовательность при
есть бесконечно малая последовательность при 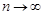 . Следовательно, последовательность
. Следовательно, последовательность 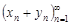 сходится и имеет предел, равный
сходится и имеет предел, равный 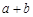 .
.
Аналогично для разности последовательностей. ◄
Теорема 4. Произведение двух сходящихся последовательностей есть сходящаяся последовательность предел которой равен произведению пределов последовательностей:
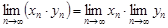 .
.
► Поскольку 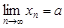
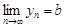 , то можно записать
, то можно записать 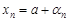 и
и 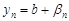 , где
, где 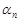 и
и 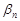 бесконечно малые последовательности при
бесконечно малые последовательности при 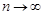 . Тогда
. Тогда
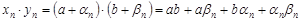 .
.
Последовательности 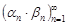 ,
, 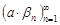 ,
, 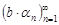 есть бесконечно малые последовательности при
есть бесконечно малые последовательности при 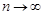 согласно свойствам бесконечно малых последовательностей. Следовательно, последовательность
согласно свойствам бесконечно малых последовательностей. Следовательно, последовательность 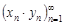 сходится и имеет предел, равный
сходится и имеет предел, равный 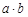 .◄
.◄
Теорема 5. Частное двух сходящихся последовательностей  и
и 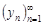 ,
, 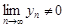 , есть сходящаяся последовательность, предел которой равен частному пределов последовательностей:
, есть сходящаяся последовательность, предел которой равен частному пределов последовательностей:
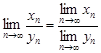 .
.
►Поскольку 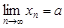
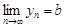 , то можно записать
, то можно записать 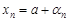 и
и 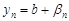 , где
, где 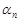 и
и 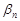 бесконечно малые последовательности при
бесконечно малые последовательности при 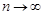 . Тогда
. Тогда
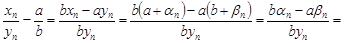
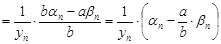 .
.
Последовательность 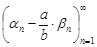 является бесконечно малой в силу свойств бесконечно малых последовательностей.
является бесконечно малой в силу свойств бесконечно малых последовательностей.
Покажем, что последовательность 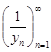 есть ограниченная последовательность.
есть ограниченная последовательность.
По определению предела имеем
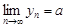
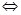
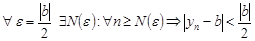 .
.
Тогда
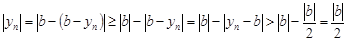 ,т.е.
,т.е. 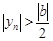 .
.
Отсюда 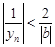 для любого
для любого 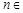
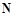 .
.
По свойству бесконечно малых последовательностей, последовательность 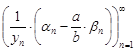 есть бесконечно малая последовательность.
есть бесконечно малая последовательность.
Следовательно, последовательность 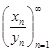 является сходящейся и
является сходящейся и 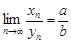 . ◄
. ◄
 2015-04-17
2015-04-17 1690
1690
