Теорема 1 (Тейлора) Функция  , однозначная и аналитическая в круге
, однозначная и аналитическая в круге 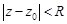 , единственным образом разлагается в этом круге в ряд Тейлора
, единственным образом разлагается в этом круге в ряд Тейлора
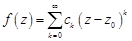 ,где
,где 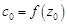 ,
, 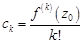 ,
, 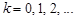 .
.
Коэффициенты 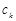 , учитывая интеграл типа Коши (практическое занятие 5), можно вычислять по формулам
, учитывая интеграл типа Коши (практическое занятие 5), можно вычислять по формулам 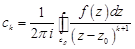 ,
, 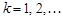 ,где
,где 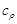 – произвольная окружность с центром в точке
– произвольная окружность с центром в точке 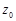 .
.
Говорят, что функция  голоморфна в точке
голоморфна в точке 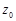 , если она в некоторой окрестности этой точки раскладывается в ряд по степеням (
, если она в некоторой окрестности этой точки раскладывается в ряд по степеням (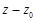 ). Функция, голоморфная в каждой точке области
). Функция, голоморфная в каждой точке области 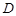 , называется голоморфной в этой области.
, называется голоморфной в этой области.
Особой точкой функции  называется точка, в которой функция не является аналитической.
называется точка, в которой функция не является аналитической.
При 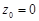 имеет место ряд Маклорена:
имеет место ряд Маклорена: 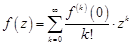 .
.
Разложения в ряд Маклорена некоторых элементарных функций комплексной переменной аналогичны разложениям в ряд Тейлора функций действительной переменной:
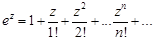 ,
, 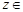
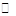 ,
,
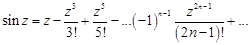 ,
, 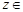
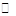 ,
,
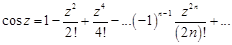 ,
, 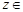
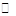 ,
,
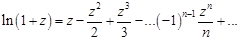 ,
, 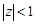 ,
,
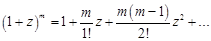 ,
, 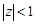 .
.
Ряд Тейлора для многозначной функции получается из разложения соответствующей однозначной функции путем прибавления к нему чисел 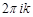 ,
, 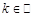 .
.
Вопрос 5 Несобственные интегралы. Признаки сходимости несобственных интегралов.
5.1. Несобственные интегралы с бесконечными пределами интегрирования (первого рода). Пусть функция  непрерывна на промежутке
непрерывна на промежутке 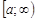 . Тогда она будет непрерывной на любом конечном отрезке
. Тогда она будет непрерывной на любом конечном отрезке  ,
, 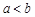 . Для функции
. Для функции  непрерывной на
непрерывной на  , существует определенный интеграл
, существует определенный интеграл 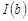 , зависящий от верхнего предела интегрирования:
, зависящий от верхнего предела интегрирования:
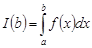 .
.
Этот интеграл определяет некоторую величину, например площадь криволинейной трапеции, ограниченной графиком функции 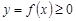 , прямыми
, прямыми 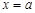 ,
, 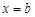 и осью абсцисс. Будем неограниченно увеличивать верхний предел интегрирования (
и осью абсцисс. Будем неограниченно увеличивать верхний предел интегрирования (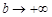 ). При этом возможны два случая: либо
). При этом возможны два случая: либо 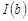 при
при 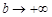 имеет предел, либо не имеет.
имеет предел, либо не имеет.
Определение 1. Несобственным интегралом с бесконечным верхнимпределом интегрирования, от непрерывной функции  на промежутке
на промежутке 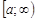 называется предел
называется предел 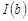 при
при 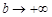 :
:
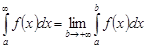 .
.
Если существует конечный предел 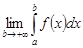 , то несобственный интеграл
, то несобственный интеграл 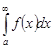 называется сходящимся, если этот предел не существует, то – расходящимся.
называется сходящимся, если этот предел не существует, то – расходящимся.
Аналогично определяется несобственный интеграл с бесконечным нижним пределоминтегрирования от непрерывной функции  на промежутке
на промежутке 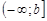 .
.
Определение 2. Несобственным интегралом с бесконечным нижним пределом интегрирования, от непрерывной функции  на промежутке
на промежутке 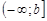 называется предел
называется предел 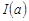 при
при 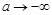 :
:
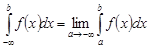 .
.
Если существует конечный предел 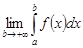 , то несобственный интеграл
, то несобственный интеграл 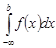 называется сходящимся, если этот предел не существует, то – расходящимся.
называется сходящимся, если этот предел не существует, то – расходящимся.
Несобственный интеграл с двумя бесконечными пределами интегрированияот непрерывной функции  на промежутке
на промежутке 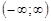 , обозначаемый
, обозначаемый 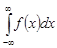 , предварительно представляют в виде
, предварительно представляют в виде
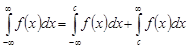 ,
, 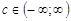 .
.
Тогда по определению
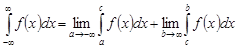 .
.
причем этот несобственный интеграл называется сходящимся, если оба предела существуют. Если хотя бы один из пределов не существует или бесконечен, то несобственный интеграл 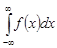 называется расходящимся.
называется расходящимся.
Интегралы 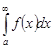 ,
, 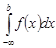 ,
, 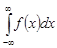 называются также несобственными интегралами первого рода.
называются также несобственными интегралами первого рода.
С геометрической точки зрения сходящийся несобственный интеграл 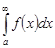 означает, что фигура, ограниченная кривой
означает, что фигура, ограниченная кривой 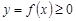 , прямыми
, прямыми 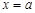 ,
, 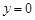 и бесконечно вытянутая в направлении оси
и бесконечно вытянутая в направлении оси 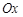 , имеет конечную площадь
, имеет конечную площадь 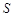 (рис.1).
(рис.1).
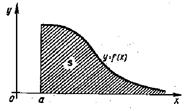
Рис.1.Геометрический смысл сходящегося несобственного
интеграла с бесконечным верхним пределом
Аналогичная геометрическая интерпретация имеет место для двух других сходящихся несобственных интегралов.
Примеры. Вычислить интегралы 1) 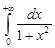 , 2)
, 2) 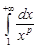 .
.
Решение. 1. Имеем
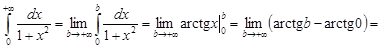
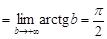 .
.
2. При 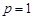 имеем
имеем
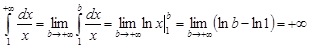 .
.
При 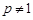 получим
получим
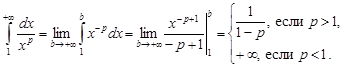
Следовательно, интеграл 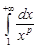 сходится при
сходится при 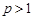 и расходится при
и расходится при 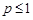 .
.
Определение 3. Интегралом в смысле главного значения называется интеграл:
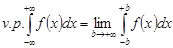 ,
, 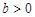 . (1)
. (1)
Отличие интеграла в смысле главного значения от несобственного интеграла состоит в том, что несобственный интеграл есть
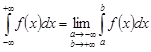 (2)
(2)
при произвольных 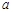 и
и 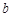 , а интеграл в смысле главного значения (1) есть предел того же интеграла, но при
, а интеграл в смысле главного значения (1) есть предел того же интеграла, но при 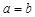
Очевидно, что, если существует несобственный интеграл (2), то и существует интеграл в смысле главного значения (1). Обратное верно не всегда: интеграл в смысле главного значения (1) может существовать, а несобственный интеграл (2) – нет.
5.2. Несобственные интегралы от неограниченных функций (второго рода). Пусть функция  определена на промежутке
определена на промежутке 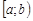 и неограничена в левосторонней окрестности точки
и неограничена в левосторонней окрестности точки 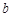 (
(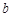 – точка бесконечного разрыва), т.е.
– точка бесконечного разрыва), т.е. 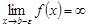 . Будем считать, что функция
. Будем считать, что функция  интегрируема на отрезке
интегрируема на отрезке 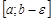 для любого
для любого 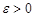 : существует интеграл
: существует интеграл 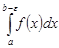 , зависящий от переменного верхнего предела интегрирования.
, зависящий от переменного верхнего предела интегрирования.
Определение 4. Несобственным интегралом второго рода от функции  непрерывной на промежутке
непрерывной на промежутке 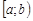 и имеющей бесконечный разрыв в точке
и имеющей бесконечный разрыв в точке 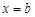 называется предел интеграла
называется предел интеграла 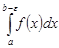 при
при 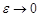 :
:
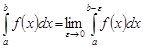 ,
, 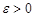 .
.
Аналогично если функция  имеет бесконечный разрыв в точке
имеет бесконечный разрыв в точке 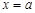 .
.
Определение 5. Несобственным интегралом второго рода от функции  непрерывной на промежутке
непрерывной на промежутке 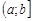 и имеющей бесконечный разрыв в точке называется предел интеграла
и имеющей бесконечный разрыв в точке называется предел интеграла 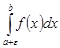 при
при 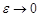 :
:
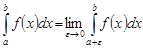 ,
, 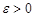 .
.
Если же функция  имеет разрыв второго рода в некоторой внутренней точке
имеет разрыв второго рода в некоторой внутренней точке 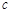 отрезка
отрезка  , то, пользуясь свойством аддитивности определенного интеграла, данный интеграл необходимо представить в виде суммы двух интегралов:
, то, пользуясь свойством аддитивности определенного интеграла, данный интеграл необходимо представить в виде суммы двух интегралов:
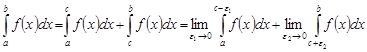 .
.
Если пределы в правых частях формул существуют и конечны, то соответствующие несобственные интегралы от разрывной функции в точках 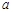 ,
, 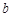 и
и 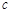 называются сходящимися, в противном случае – расходящимися.
называются сходящимися, в противном случае – расходящимися.
С геометрической точки зрения сходящийся несобственный интеграл второго рода означает, что фигура, ограниченная кривой 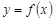 , прямыми
, прямыми 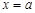
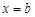 и бесконечно вытянутая в направлении оси
и бесконечно вытянутая в направлении оси 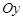 при
при 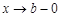 (
(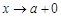 ,
, 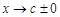 ), имеет конечную площадь
), имеет конечную площадь 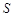 (Рис.2, а – в соответственно).
(Рис.2, а – в соответственно).
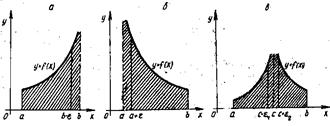
Рис.2.Геометрический смысл несобственных
Интегралов от неограниченных функций
Пример. Вычислить интеграл 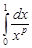 .
.
Решение. При 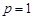 имеем:
имеем:
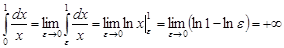 .
.
При 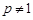 имеем
имеем
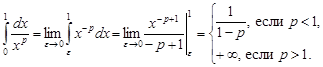
Следовательно, интеграл 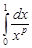 сходится при
сходится при 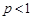 и расходится при
и расходится при 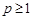 .
.
5.3. Формулы интегрального исчисления для несобственных интегралов. В силу свойств предела функции и определения несобственного интеграла как предела функции, являющейся интегралом Римана с переменным пределом интегрирования, многие свойства определенного интеграла предельным переходом переносятся на несобственные интегралы. Для простоты будем рассматривать случай несобственного интеграла от функций, определенных на полуинтервале 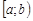 и интегрируемых по Риману на любом отрезке
и интегрируемых по Риману на любом отрезке 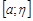 ,
, 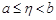 .
.
Формула Ньютона-Лейбница.Если функция  непрерывна на промежутке
непрерывна на промежутке 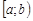 и
и 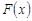 – какая-либо ее первообразная, то
– какая-либо ее первообразная, то
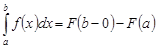 .
.
Линейность интеграла. Если несобственные интегралы 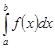 и
и 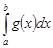 сходятся, то для любых чисел
сходятся, то для любых чисел 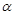 и
и 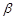 несобственный интеграл
несобственный интеграл 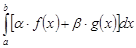 также сходится и
также сходится и
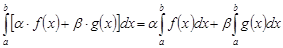 .
.
Интегрирование неравенств.Если несобственные интегралы 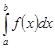 и
и 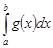 сходятся и для всех
сходятся и для всех 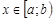 выполняется неравенство
выполняется неравенство 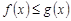 , то
, то
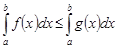 .
.
Правило замены переменной.Если функция  непрерывна на промежутке
непрерывна на промежутке 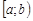 , функция
, функция 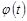 непрерывно дифференцируема на промежутке
непрерывно дифференцируема на промежутке 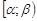 ,
, 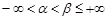 , и выполняются условия
, и выполняются условия 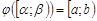 ,
, 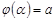 ,
, 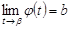 , то
, то
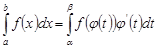 .
.
Правило интегрирования по частям.Пусть 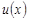 и
и 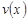 непрерывны на промежутке
непрерывны на промежутке 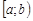 , а их производные
, а их производные 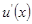 и
и 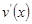 кусочно-непрерывны на любом отрезке
кусочно-непрерывны на любом отрезке 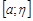 ,
, 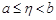 . Тогда
. Тогда
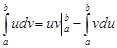 .
.
Пример. Вычислить интеграл 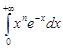 ,
, 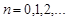 .
.
Решение. Проинтегрируем по частям
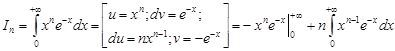 ,
,
т.е. 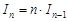 .
.
Поскольку 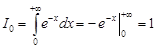 , то, применяя последовательно рекуррентную формулу, получим
, то, применяя последовательно рекуррентную формулу, получим
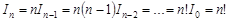 .
.
 2015-04-17
2015-04-17 3363
3363








