Критерий Коши сходимости несобственного интеграла

Теорема 1 (критерий Коши). Несобственный интеграл 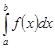сходится тогда и только тогда, когда для любого 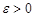существует такое 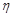, что для всех 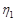и 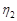, удовлетворяющих условию 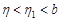, , 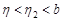выполняется неравенство .

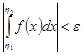► Положим 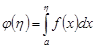. Сходимость интеграла 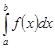означает существование конечного предела функци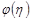и при 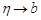. Согласно критерию Коши существования предела 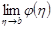необходимо и достаточно, чтобы для любого 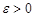нашлось такое 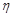, что для всех 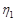и 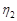, удовлетворяющих условию 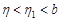, , 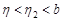выполняется неравенство

.

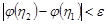Поскольку ,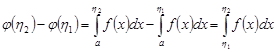

то получаем . ◄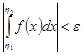

5.4. Признаки сравнения несобственных интегралов. Будем рассматривать случай несобственного интеграла от функций, определенных на полуинтервале 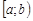и интегрируемых по Риману на любом отрезке 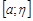, 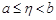(несобственный интеграл 1-го или 2-го рода)

Лемма 1. Если функция неотрицательна на интервале 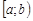, то для сходимости несобственного интеграла 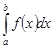необходимо и достаточно, чтобы множество всех интегралов 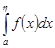, , 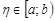было ограничено сверху, т.е. чтобы существовала такая постоянная 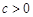, что для всех 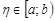выполнялось неравенство

.

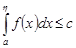Без доказательства.

Теорема 1 (признак сравнения). Пусть на промежутке 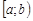определены две неотрицательные функции и 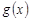, интегрируемые на каждом конечном отрезке 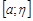, , 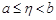причем 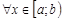справедливо 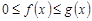. Тогда

1) из сходимости интеграла 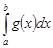следует сходимость интеграла ,

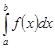2) из расходимости интеграла 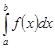следует расходимость интеграла .

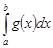► Для любого 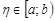имеем .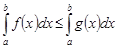

Случай 1. Если интеграл 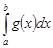сходится, то согласно лемме 1 интегралы 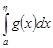, , 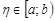ограничены сверху. Значит, и интегралы 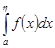также ограничены сверху. По лемме 1 интеграл 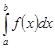сходится.

Случай 2. Если интеграл 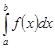расходится, то в силу доказанного 1) интеграл 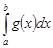не может сходится. Если бы он сходился, то и интеграл 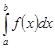также сходился бы. Значит, интеграл 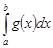расходится. ◄

Следствие 1 (предельный признак сравнения). Пусть на промежутке 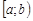определены две неотрицательные функции и 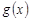, интегрируемые на каждом конечном отрезке 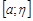, , 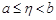причем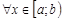 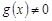, и существует конечный предел

.

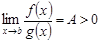Тогда 1) если интеграл 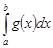сходится и 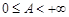, то интеграл 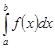сходится,

2) если интеграл 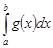расходится и 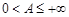, то интеграл 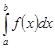расходится,

3) если 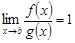, то интегралы 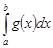и 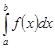сходятся или расходятся одновременно.

Без доказательства.

Примеры. Исследовать на сходимость интегралы

1) 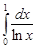, 2) .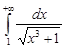

Решение. 1. Сравним интеграл 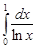с расходящимся интегралом 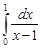. Поскольку 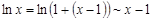при 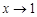, то имеем

.

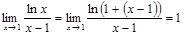Значит, интеграл 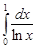расходится.

2. Сравним данный интеграл со сходящимся интегралом 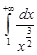. Поскольку

,

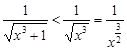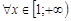
то из сходимости интеграла 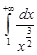согласно признаку сравнения следует, что интеграл 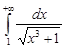сходится.