Абсолютная сходимость

Определение 1. Несобственный интеграл 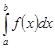называется абсолютно сходящимся интегралом, если сходится интеграл .

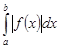Теорема 2 (критерий Коши абсолютной сходимости интеграла). Несобственный интеграл 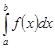абсолютно сходится тогда и только тогда, когда для любого 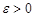существует такое 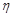, что для всех 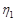и 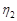, удовлетворяющих условию 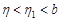, , 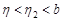выполняется неравенство .

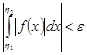Без доказательства.

Теорема 3. Если несобственный интеграл 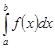абсолютно сходится, то он сходится.

► Если несобственный интеграл 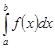абсолютно сходится, то по теореме 2 для любого 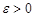существует такое 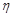, что для всех 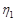и 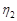, удовлетворяющих условию 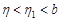, , 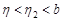выполняется неравенство .

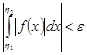Тогда

.

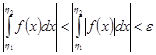В силу критерия Коши для сходимости интеграла, интеграл 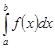сходится. ◄

Замечание. Обратное верно не всегда.

Пример. Исследовать на сходимость интегралы:

1) 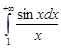, 2) .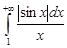

Решение. 1. Имеем

.

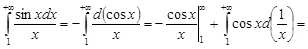
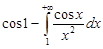Поскольку 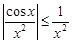и интеграл 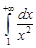сходится, то интеграл 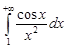абсолютно сходится. Следовательно, интеграл 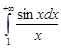сходится.

2. Из неравенства

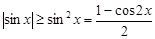
следует, что для любого 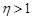выполняется неравенство

.

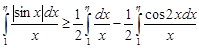Интеграл 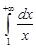расходится.

Интеграл 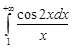сходится, поскольку

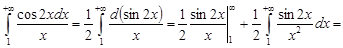
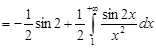
и интеграл 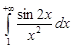сходится, поскольку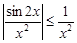

и интеграл 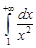сходящийся, 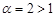. Значит, интеграл 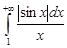расходится.