Признаки Дирихле и Абеля

Теорема 4 (признак Дирихле). Пусть на полуоси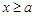

1) функция непрерывна и имеет ограниченную первообразную,

2) функция 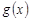непрерывно дифференцируема и .

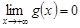Тогда интеграл 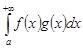сходится.

Пример. Исследовать на сходимость интеграл , .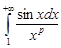

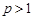Решение. Функция 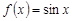имеет ограниченную первообразную 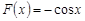, а функция 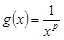, , 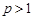убывает при 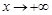, т.е. 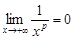. Согласно признаку Дирихле интеграл 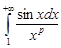сходится.

Теорема 5 (признак Абеля). Пусть на полуоси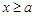

1) функция непрерывна и интеграл 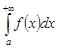сходится,

2) функция 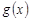непрерывно дифференцируема, ограничена и монотонна.

Тогда интеграл 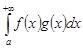сходится.

Пример. Исследовать на сходимость интеграл

, .

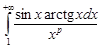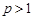Решение. Интеграл 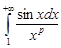, , 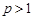сходится, а функция 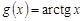ограничена и монотонна. В силу признака Абеля интеграл

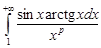
сходится.

Вопрос 6 Интеграл функции комплексного переменного. Интегральная теорема Коши. Интегральная формула Коши.