Теорема 1 (интегральная формула Коши) Пусть функция 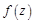 аналитична в области
аналитична в области 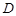 . Тогда для любой точки
. Тогда для любой точки 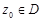 справедливо равенство
справедливо равенство
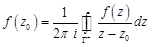 ,
,
где 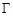 – кусочно-гладкий замкнутый контур, целиком лежащий в области
– кусочно-гладкий замкнутый контур, целиком лежащий в области 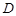 и охватывающий точку
и охватывающий точку 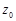 .
.
Интеграл 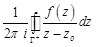 , стоящий в правой части равенства теоремы 1, называется интегралом Коши функции
, стоящий в правой части равенства теоремы 1, называется интегралом Коши функции 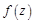 .Если в условиях теоремы точка
.Если в условиях теоремы точка 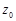 расположена вне области, ограниченной контуром
расположена вне области, ограниченной контуром 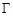 , то
, то
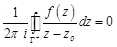 .
.
Теорема 2 (о среднем) Значение аналитической функции 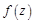 в любой точке
в любой точке 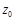 области
области 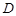 , в которой функция
, в которой функция 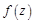 является аналитической, равно среднему арифметическому ее значений на любой окружности с центром в точке
является аналитической, равно среднему арифметическому ее значений на любой окружности с центром в точке 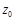 , целиком лежащей в области
, целиком лежащей в области 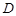 .
.
Пусть функция 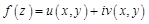 аналитическая в односвязной области
аналитическая в односвязной области 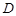 . Если в области
. Если в области 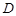 постоянна действительная часть
постоянна действительная часть 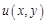 функции
функции 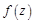 или постоянен модуль функции
или постоянен модуль функции 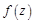 , то функция
, то функция 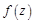 постоянна в области
постоянна в области 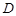 .
.
Теорема 3 (о максимуме модуля) Пусть функция 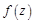 , не равная тождественно постоянной, является аналитической в области
, не равная тождественно постоянной, является аналитической в области 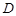 и непрерывна в
и непрерывна в 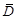 . Тогда максимальное (минимальное) значение модуля
. Тогда максимальное (минимальное) значение модуля 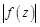 достигается только на границе области
достигается только на границе области 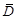 .
.
Другими словами, модуль 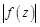 не может достигать максимума (минимума) внутри области
не может достигать максимума (минимума) внутри области 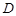 кроме случая, когда
кроме случая, когда 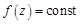 .
.
Вопрос 7 Ряд Лорана. Особые точки аналитической функции.
 2015-04-17
2015-04-17 612
612







