Теорема 1. Если функция 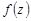 комплексного переменного
комплексного переменного 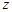 непрерывна на гладкой кривой
непрерывна на гладкой кривой  , заданной параметрическими уравнениями
, заданной параметрическими уравнениями 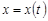 ,
, 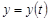 , а начальная и конечная точка дуги соответствуют значениям
, а начальная и конечная точка дуги соответствуют значениям 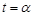 и
и 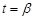 , то интеграл
, то интеграл 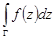 существует и справедлива формула
существует и справедлива формула
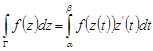 , где
, где 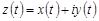 ,
, 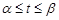 .
.
Теорема 2. Если функция 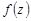 комплексного переменного
комплексного переменного 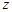 непрерывна на гладкой кривой
непрерывна на гладкой кривой  , то интеграл
, то интеграл 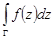 существует и справедлива формула
существует и справедлива формула
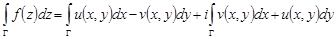 .
.
► Пусть  непрерывна на кривой
непрерывна на кривой  , уравнение которой
, уравнение которой  ,
, 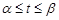 .
.
Тогда
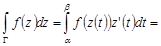
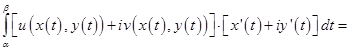
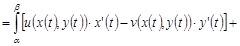
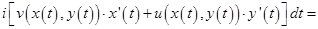
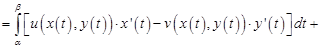
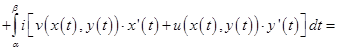
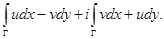 ◄
◄
Следствие. 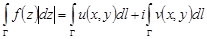 , где
, где 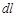 – дифференциал длины дуги кривой
– дифференциал длины дуги кривой  .
.
Пример. Вычислить интеграл 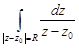 , где обход окружности осуществляется в положительном направлении.
, где обход окружности осуществляется в положительном направлении.
Решение. Параметрические уравнения окружности с центром в точке  есть
есть
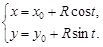
Отсюда получим комплексно-параметрическое уравнение окружности
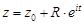 , где
, где  .
.
Тогда
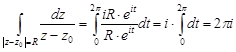 .
.
6.3. Свойства интегралов по комплексному переменному. Интегралы от комплексного переменного обладают следующими свойствами.
1 (линейность). Если 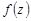 и
и 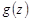 непрерывны на кусочно-гладкой кривой
непрерывны на кусочно-гладкой кривой  , то для любых комплексных постоянных
, то для любых комплексных постоянных 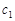 и
и 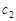
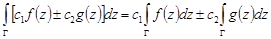 .
.
2 (ориентированность). Пусть 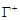 и
и 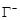 — один и тот же путь интегрирования, проходимый соответственно в положительном и отрицательном направлении кусочно-гладкой кривой
— один и тот же путь интегрирования, проходимый соответственно в положительном и отрицательном направлении кусочно-гладкой кривой  , и функция
, и функция 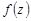 непрерывна на этой кривой. Тогда
непрерывна на этой кривой. Тогда
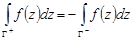 .
.
3 (аддитивность). Пусть кривая  состоит из кусочно-гладких кривых
состоит из кусочно-гладких кривых 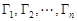 и функция
и функция 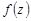 непрерывна на
непрерывна на  . Тогда
. Тогда
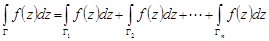 ,
,
причем направление на кривых 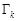 ,
, 
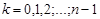 , совпадает с направлением на кривой
, совпадает с направлением на кривой  .
.
4. Если  – произвольная кусочно-гладкая кривая с началом
– произвольная кусочно-гладкая кривая с началом 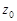 и концом
и концом 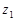 , то
, то 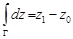 .
.
5. Если  – гладкая кривая, замкнутая или незамкнутая, имеющая длину
– гладкая кривая, замкнутая или незамкнутая, имеющая длину 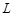 , то
, то 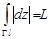 .
.
6 (оценка интеграла). Для любой функции 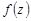 , непрерывной на гладкой кривой
, непрерывной на гладкой кривой  , справедливо неравенство
, справедливо неравенство
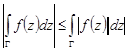 .
.
7. Если 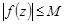 во всех точках гладкой кривой
во всех точках гладкой кривой  , то справедливо неравенство
, то справедливо неравенство
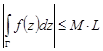 , где
, где 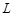 – длина кривой
– длина кривой  .
.
6.4. Основная теорема Коши. Пусть функция 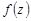 является аналитической в односвязной области
является аналитической в односвязной области 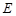 .
.
Теорема 3 (Коши). Если функция 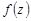 аналитична в односвязной области
аналитична в односвязной области 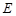 , то интеграл от этой функции по любому кусочно-гладкому замкнутому контуру
, то интеграл от этой функции по любому кусочно-гладкому замкнутому контуру  , целиком лежащему в области
, целиком лежащему в области 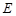 , равен нулю
, равен нулю
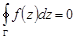 .
.
► Предположим, что 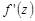 непрерывна. Пусть
непрерывна. Пусть  — какой-нибудь кусочно-гладкий замкнутый контур, целиком лежащий в области
— какой-нибудь кусочно-гладкий замкнутый контур, целиком лежащий в области 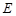 и
и 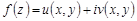 . Тогда согласно теореме 2 имеем
. Тогда согласно теореме 2 имеем
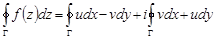 .
.
В силу условий Коши – Римана в области 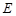 имеем
имеем
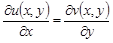 ,
, 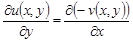 .
.
Из непрерывности 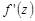 в области
в области 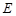 вытекает непрерывность частных производных первого порядка по
вытекает непрерывность частных производных первого порядка по 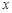 и по
и по 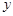 от функций
от функций 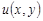 и
и 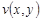 . Так как функции
. Так как функции 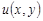 и
и 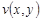 непрерывно дифференцируемы в области
непрерывно дифференцируемы в области 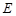 , удовлетворяют в ней равенствам Коши-Римана и область
, удовлетворяют в ней равенствам Коши-Римана и область 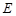 односвязна, то, с учетом формулы Грина, получим
односвязна, то, с учетом формулы Грина, получим
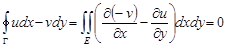 ,
, 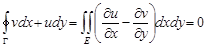 .
.
Отсюда получаем 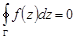 . ◄
. ◄
Теорема Коши для многосвязной области. Теорема Коши допускает распространение на случай многосвязной области.
Рассмотрим для определенности трехсвязную область 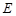 , ограниченную внешним контуром
, ограниченную внешним контуром  и внутренними контурами
и внутренними контурами 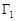 и
и 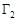 . Выберем положительное направление обхода контуров: при обходе область
. Выберем положительное направление обхода контуров: при обходе область 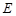 остается слева (см. рис.2).
остается слева (см. рис.2).
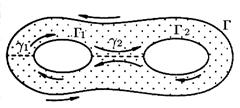
Рис.2.
Пусть функция 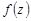 аналитична в области
аналитична в области 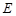 и на контурах
и на контурах  ,
, 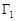 и
и 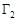 , (т. е. в замкнутой области
, (т. е. в замкнутой области 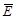 ). Проведя два разреза (две дуги)
). Проведя два разреза (две дуги) 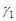 и
и 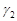 области
области 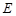 (см.рис.2), получим новую односвязную область
(см.рис.2), получим новую односвязную область 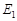 , ограниченную замкнутым ориентированным контуром
, ограниченную замкнутым ориентированным контуром 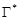 , состоящим из контуров
, состоящим из контуров  ,
, 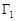 ,
, 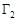 и разрезов
и разрезов 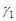 и
и 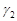 :
:
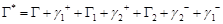 .
.
По теореме Коши для односвязной области
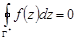 .
.
Учитывая
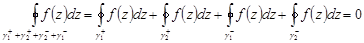 ,
,
т. к. каждый из разрезов (дуг) 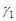 и
и 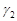 при интегрировании проходится дважды в противоположных направлениях. Поэтому получаем:
при интегрировании проходится дважды в противоположных направлениях. Поэтому получаем:
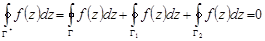
т. е. интеграл от аналитической в замкнутой многосвязной области функции 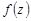 по границе области
по границе области 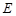 , проходимой в положительном направлении, равен нулю.
, проходимой в положительном направлении, равен нулю.
Замечание. Изменив направление обхода внутренних контуров 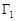 ,
, 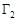 будем иметь
будем иметь
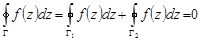
где все контуры  ,
, 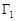 ,
, 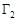 обходятся в одном направлении: против часовой стрелки (или по часовой стрелке). В частности, если
обходятся в одном направлении: против часовой стрелки (или по часовой стрелке). В частности, если 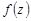 аналитична в двусвязной области, ограниченной контурами
аналитична в двусвязной области, ограниченной контурами  и
и 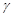 и на самих этих контурах (см. рис.3), то
и на самих этих контурах (см. рис.3), то
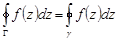 ,
,
т.е. «интеграл от функции 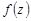 по внешнему контуру
по внешнему контуру  равен интегралу от функции
равен интегралу от функции 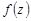 по внутреннему контуру
по внутреннему контуру 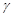 (контуры
(контуры  и
и 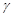 обходятся в одном направлении).
обходятся в одном направлении).
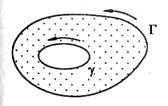 Рис.3. Рис.3. | 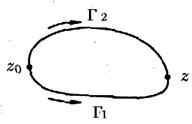 Рис.4. Рис.4. |
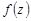 — аналитическая функция в односвязной области
— аналитическая функция в односвязной области 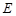 . Тогда интеграл от функции
. Тогда интеграл от функции 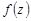 не зависит от формы пути интегрирования, а зависит лишь от начальной точки
не зависит от формы пути интегрирования, а зависит лишь от начальной точки 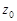 и конечной точки
и конечной точки 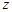 пути интегрирования.
пути интегрирования.
► Пусть 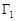 и
и 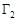 две кривые в области
две кривые в области 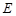 , соединяющей точки
, соединяющей точки 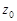 и
и 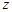 (рис.4). По теореме Коши
(рис.4). По теореме Коши
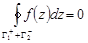 .
.
С другой стороны, по свойствам интеграла
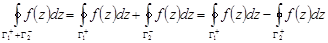 .
.
Следовательно, 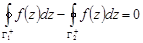 .
.
Откуда 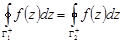 . ◄
. ◄
 2015-04-17
2015-04-17 1836
1836
