Пусть. Пусть 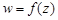 — однозначная функция комплексного переменного
— однозначная функция комплексного переменного 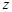 , определенная на некоторой гладкой кривой
, определенная на некоторой гладкой кривой  с началом в точке
с началом в точке 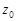 и концом в точке
и концом в точке 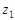 . Кривая
. Кривая  может быть как замкнутой, так и незамкнутой. Направление движения по кривой
может быть как замкнутой, так и незамкнутой. Направление движения по кривой  от начальной точки
от начальной точки 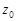 к конечной точке
к конечной точке 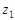 называется положительным направлением на кривой
называется положительным направлением на кривой  и обозначается через
и обозначается через 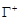 . Противоположное направление на кривой
. Противоположное направление на кривой  называется отрицательным и обозначается
называется отрицательным и обозначается 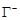 .
.
Разобьем кривую  на
на 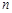 частичных дуг произвольно выбранными точками
частичных дуг произвольно выбранными точками 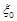 ,
, 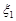 ,
, 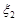 ,
, 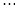 ,
, 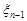 ,
, 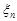 , причем
, причем 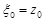 ,
, 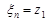 , расположенными последовательно в положительном направлении кривой
, расположенными последовательно в положительном направлении кривой  (рис. 1).
(рис. 1).
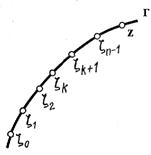
Рис.1. Разбиение кривой 
На каждой частичной дуге 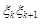 ,
, 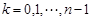 , выберем произвольную точку
, выберем произвольную точку 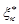 и составим интегральную сумму
и составим интегральную сумму
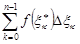 , где
, где 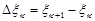 .
.
Определение 1. Комплексное число 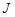 называется пределом интегральных сумм
называется пределом интегральных сумм 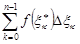 , при
, при 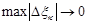 , если для любого
, если для любого 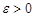 найдется такое
найдется такое 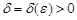 , что при любом разбиении кривой
, что при любом разбиении кривой  на частичные дуги
на частичные дуги 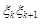 ,
, 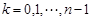 , и при любом выборе точек
, и при любом выборе точек 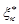 на частичных дугах
на частичных дугах 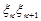 имеет место неравенство
имеет место неравенство 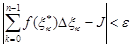 при
при 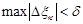 .
.
Определение 2. Предел интегральных сумм 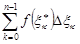 при
при 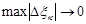 , если он существует, называется интегралом от функции
, если он существует, называется интегралом от функции 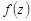 вдоль кривой
вдоль кривой  (в выбранном направлении).
(в выбранном направлении).
Обозначается: 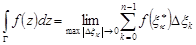 .
.
Если для функции 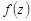 , определенной на кривой
, определенной на кривой  , данный предел существует, то говорят, что функция
, данный предел существует, то говорят, что функция 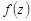 интегрируема по кривой
интегрируема по кривой  . Кривая
. Кривая  называется путем или контуром интегрирования.
называется путем или контуром интегрирования.
Интеграл от функции 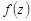 в положительном направлении кривой
в положительном направлении кривой  обозначается
обозначается 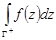 . Интеграл от функции
. Интеграл от функции 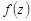 в отрицательном направлении кривой
в отрицательном направлении кривой  – символом
– символом 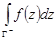 . В случае замкнутого контура
. В случае замкнутого контура  интеграл от функции
интеграл от функции 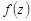 по кривой
по кривой  обозначается символом
обозначается символом 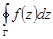 .
.
Положительным направлением обхода замкнутого простого контура  считается такое направление движения, при котором область, ограниченная данным замкнутым контуром и находящаяся внутри контура
считается такое направление движения, при котором область, ограниченная данным замкнутым контуром и находящаяся внутри контура  , остается слева от направления движения. Противоположное направление обхода замкнутого контура
, остается слева от направления движения. Противоположное направление обхода замкнутого контура  называется отрицательным. Интеграл по замкнутому контуру
называется отрицательным. Интеграл по замкнутому контуру  в положительном направлении обозначается
в положительном направлении обозначается 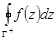 , интегрирование в отрицательном направлении – символом
, интегрирование в отрицательном направлении – символом 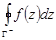 .
.
 2015-04-17
2015-04-17 829
829








