На плоскости и в пространстве

1. Декартова прямоугольная система координат на плоскости

2 Предположим, что на произвольной прямой линии выбрано одно из двух направлений. Выбранное направление называют положительным и отмечают в виде стрелки. Прямую линию, с выбранным на ней положительным направлением, называют осью. Пусть на оси отмечена фиксированная точка О (начало координат) и выбран единичный отрезок (масштаб), с помощью которого измеряют расстояния между точками на прямой. Ось, с выбранным на ней началом координат и единичным отрезком, называют числовой осью.

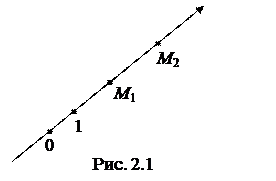Пусть на числовой оси имеются две точки М ₁ и М ₂ (рис. 2.1). Величиной направленного отрезка (сокращенно обозначается вел. ), называется его длина, взятая со знаком плюс, если направление от точки М ₁ к точке М ₂ совпадает с направлением оси и со знаком минус,– в противном случае.

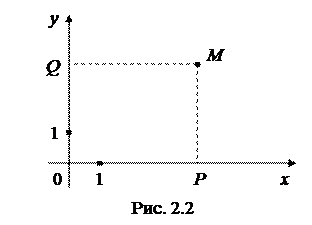2 Декартовой прямоугольной системой координат на плоскости называются две взаимно перпендикулярные числовые оси, имеющие общее начало координат и одинаковый масштаб. Обычно одну из осей изображают горизонтально и называют осью абсцисс (ось Ox), а другую – вертикально и называют осью ординат (ось Oy). Точка пересечения осей координат (точка О) называется началом координат.

Пусть на плоскости выбрана система координат, и пусть М – произвольная точка плоскости. Опустим перпендикуляры из точки М на оси координат (спроектируем точку на оси координат). Мы получим точки P и Q. Величину направленного отрезка 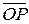называют иксовой координатой или абсциссой точки М, величину направленного отрезка 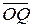называют игрековой координатой или ординатой точки М. Обычно координаты точки записывают в круглых скобках рядом с обозначением самой точки: М (x; y), где x = вел. 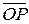, y = вел. .

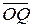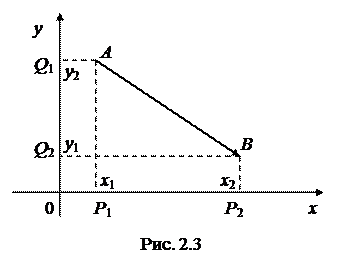Предположим теперь, что на плоскости имеется вектор (направленный отрезок) (рис. 2.3). Точка А – начало вектора, точка В – его конец.

Координатами вектора называются проекции данного вектора на оси координат. Проекция вектора на ось Ox равна величине направленного отрезка 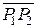оси Ox: вел. 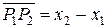. Проекция вектора 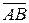на ось Oy равна величине направленного отрезка 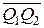оси Oy: вел. 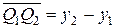. При этом (x ₁; y ₁) являются координатами точки А, а (x ₂; y ₂) – координатами точки В. Таким образом, координаты вектора 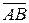равны разности координат конца и начала вектора. Координаты вектора мы будем записывать в круглых скобках рядом с вектором, через знак равенства: .

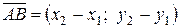В отличие от координат точки координаты вектора не позволяют однозначно определить его местоположение на плоскости. Так на
рис. 2.4 показаны два вектора и , имеющие одни и те же координаты (1; 2). Т.е. 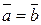. Благодаря этому обстоятельству, векторы в векторной алгебре принято считать свободными. Это означает, что векторы можно перемещать в плоскости, сохраняя при этом длину и направление.

2 2. Декартовой прямоугольной системой координат в пространстве называются три взаимно перпендикулярные числовые оси, имеющие общее начало координат и одинаковый масштаб.

В пространстве можно рассматривать две принципиально различные системы координат: левостороннюю и правостороннюю. В правосторонней системе координат кратчайший поворот от оси OX к оси OY виден из конца оси OZ против часовой стрелки. Запомнить данное правила можно при помощи правой руки (отсюда и название). При этом большому пальцу соответствует ось OZ, указательному – ось OX, а среднему – ось OY. В дальнейшем мы будем рассматривать только правостороннюю систему координат (рис. 2.5.).

z

В пространственной декартовой системе координат координаты точки и вектора определяются аналогично тому, как мы определяли их на плоскости. Отличие заключается лишь в том, что точка и вектор в пространстве будут иметь три координаты.

В дальнейшем нам понадобятся единичные векторы, расположенные на осях координат: 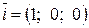– единичный вектор на оси Ox, 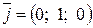– единичный вектор на оси Oy, 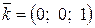– единичный вектор на оси Oz.

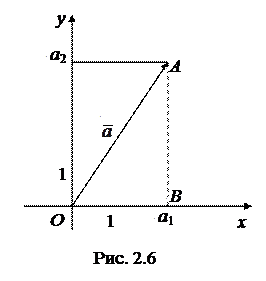Задача 2.1. Вычислить длину вектора на плоскости, зная его координаты.

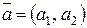Решение. Пусть вектор имеет координаты: . Длину вектора найдем по теореме Пифагора (рис. 2.6). Пользуясь тем, что вектор является свободным, поместим начало вектора в начало координат. Тогда длина вектора совпадает с длиной гипотенузы треугольника ОАВ. Длины катеты данного треугольника совпадают с абсолютными величинами координат вектора . Таким образом, .

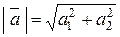В пространстве аналогичная задача решается с помощью нахождения длины диагонали прямоугольного параллелепипеда (решите ее самостоятельно). Таким образом, мы имеем две важные формулы:

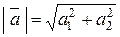, когда 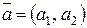. (2.1)

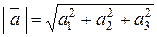, когда 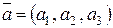. (2.2)