Существует два этапа интерпретации уравнения регрессии. Первый состоит в словесном истолковании уравнения так, чтобы это было понятно человеку, не являющемуся специалистом в области статистики. На втором этапе необходимо решить, следует ли ограничиться этим или провести более детальное исследование зависимости.
Оба этапа чрезвычайно важны. Второй этап рассмотрим несколько позже, а пока обратим внимание на первый этап.
Рассмотрим зависимость между среднедушевым потреблением и производством молока по регионам Российской Федерации, представленную на рис.3. Оценим эту зависимость как парную линейную регрессию между среднедушевым потреблением молока (у) и среднедушевым производством молока (х). То есть предположим, что истинная модель описывается выражением (8) и оценена регрессия:
| y = 120 + 0,38 x. | (27) |
Полученный результат можно истолковать следующим образом. Коэффициент при х (коэффициент наклона) показывает, что если х увеличивается на одну единицу, то y возрастает на 0,38 единицы. Как х, так и y измеряются в килограммах молока на душу населения в год; таким образом, коэффициент наклона показывает, что если производство увеличится на 1 кг/душу за год, то среднедушевое потребление молока возрастет на 0,38 кг.
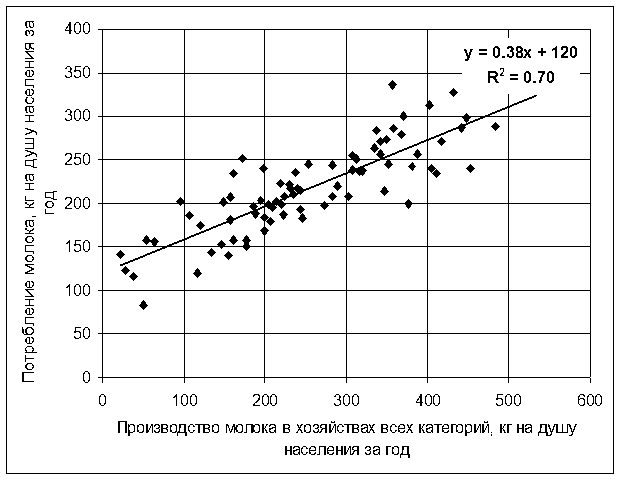
Рисунок 3 – Пример регрессионной зависимости между среднедушевым потреблением и производством молока по регионам Российской Федерации
Что можно сказать о постоянной в уравнении? Формально говоря, она показывает прогнозируемый уровень y, когда х=0. Иногда это имеет ясный смысл, иногда нет. Если х=0 находится достаточно далеко от выборочных значений хi, то буквальная интерпретация может привести к неверным результатам; даже если линия регрессии довольно точно описывает значения наблюдаемой выборки, нет гарантии, что так же будет при экстраполяции влево или вправо.
В рассматриваемом случае экстраполяция к вертикальной оси приводит к выводу о том, что если производство равно нулю, то среднедушевое потребление составило бы 120 кг. Такое толкование может быть правдоподобным в отношении отдельного региона, где отсутствуют молокоперерабатывающие предприятия. Однако такое толкование часто не имеет никакого смысла, константа выполняет единственную функцию: она позволяет определить положение линии регрессии на графике.
При интерпретации уравнения регрессии чрезвычайно важно помнить о трех вещах. Во-первых, полученные с помощью метода наименьших квадратов значения являются лишь оценками параметров модели (8). Поэтому вся интерпретация в действительности представляет собой лишь оценку. Во-вторых, уравнение регрессии отражает только общую тенденцию для выборки. При этом каждое отдельное наблюдение подвержено воздействию случайностей. В-третьих, верность интерпретации зависит от правильности спецификации уравнения.
Можно интерпретировать предсказанное значение объясняемой переменной двумя способами.
При первом способе исследователь заинтересован в оценивании значения y, для объекта, у которого х принимает значение хi. В этой ситуации 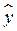 есть наилучшая оценка единственного значения y, соответствующего х = хi.
есть наилучшая оценка единственного значения y, соответствующего х = хi.
При втором подходе исследователь делает выводы о среднем значении y для совокупности объектов, у которых х = хi. Тогда та же самая оценка 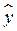 будет наилучшей оценкой среднего значения y, при х = хi.
будет наилучшей оценкой среднего значения y, при х = хi.
После оценивания регрессии возникает следующий вопрос; существуют ли какие-либо средства определения точности оценок? Этот очень важный вопрос будет рассмотрен в следующем разделе.
4.5. Качество оценки: коэффициент детерминации R2
Цель регрессионного анализа состоит в объяснении поведения зависимой переменной y. В любой выборке y оказывается уравнительно низким в одних наблюдениях и сравнительно высоким ‑ в других. Мы хотим знать, почему это так.
Разброс значений y в выборке можно описать с помощью дисперсии. Обозначим выборочную дисперсию через Var(y).
В парном регрессионном анализе мы объясняем поведение y его зависимость от х. Построив регрессионную зависимость, можно разбить значение y на две составляющие:
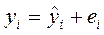 , , | (28) |
где 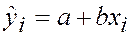 - расчетное (прогнозируемое) значение в точке i,
- расчетное (прогнозируемое) значение в точке i,
ei ‑ остаток между фактическим и cпрогнозированным значением, то есть та часть уi, мы уже не можем объяснить уравнением регрессии.
Можно доказать, что
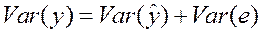 , , | (29) |
Таким образом, мы можем разложить дисперсию у на две части:
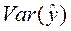 ‑ часть дисперсии, «объясненная» уравнением регрессии,
‑ часть дисперсии, «объясненная» уравнением регрессии,
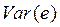 ‑ «необъясненная» уравнением регрессии часть.
‑ «необъясненная» уравнением регрессии часть.
Следовательно, 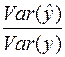 ‑ это доля дисперсии у, объясненная уравнением регрессии. Это отношение известно как коэффициент детерминации R2:
‑ это доля дисперсии у, объясненная уравнением регрессии. Это отношение известно как коэффициент детерминации R2:
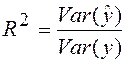 , , | (30) |
Таким образом, коэффициент детерминации, характеризует долю дисперсии у, объясненной регрессией y по x.
Из (29) получаем:
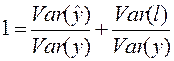 , , | (31) |
что равносильно:
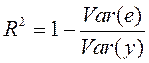 . . | (32) |
Максимальное значение коэффициента детерминации равно 1: R2=1. Это происходит в том случае, когда линия регрессии точно соответствует всем наблюдениям, то есть линия регрессии проходит точно через все yi, и все остатки равны нулю: ei=0.
Если видимая связь между y и x отсутствует, то R2 близок к 0.
Желательно, чтобы R2 был больше. То есть мы выбираем a и b так, чтобы максимизировать R2.
Это не противоречит тому, что надо минимизировать сумму квадратов отклонений 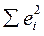 , выраженную уравнением (13).
, выраженную уравнением (13).
Действительно,
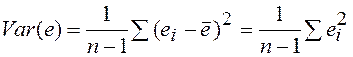 . . | (33) |
Следовательно, из выражений (32) и (33) получим:
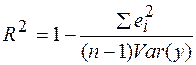 . . | (34) |
Итак, на основании выражения (34) можно сделать вывод о том, что принцип минимизации суммы квадратов 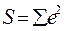 остатков эквивалентен максимизации коэффициента детерминации R2.
остатков эквивалентен максимизации коэффициента детерминации R2.
Альтернативное представление для коэффициента детерминации – представление через суммы квадратов отклонений.
Рассмотрим возможные отклонения y, связанные с моделью регрессии. Справедливо соотношение:
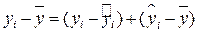 . . | (35) |
Здесь
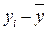 ‑ общее отклонение;
‑ общее отклонение;
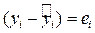 ‑ остаток;
‑ остаток;
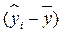 ‑ отклонение, объясненное регрессией.
‑ отклонение, объясненное регрессией.
Заметим, что
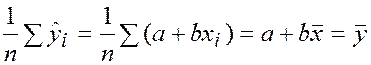 . . | (36) |
Тогда из (29) получаем:
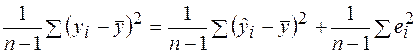 . . | (37) |
Следовательно, общая сумма квадратов отклонений равна сумме квадратов отклонений, объясненных регрессией плюс сумма квадратов остатков:
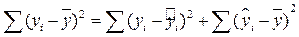 . . | (38) |
Здесь
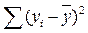 ‑ общая сумма квадратов отклонений;
‑ общая сумма квадратов отклонений;
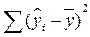 ‑ сумма квадратов отклонений, объясненных регрессией;
‑ сумма квадратов отклонений, объясненных регрессией;
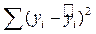 ‑ сумма квадатов остатков.
‑ сумма квадатов остатков.
Выражение для коэффициента детерминации через суммы квадратов отклонений будет иметь вид:
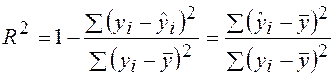 . . | (39) |
На интуитивном уровне представляется очевидным, что чем больше соответствие, обеспечиваемое уравнением регрессии, то есть между фактическим и прогнозным значениями объясняемой переменной y, тем больше должен быть коэффициент корреляции 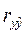 между y и
между y и 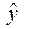 .
.
Можно доказать, что коэффициент детерминации равен квадрату коэффициента корреляции между фактическим и прогнозным значениями y:
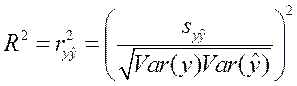 . . | (40) |
Здесь 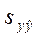 ‑ выборочная ковариация между y и
‑ выборочная ковариация между y и 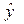 .
.
 2015-04-01
2015-04-01 6471
6471
