Под точностью измерений понимают качество измерений, определяющее близость их результатов к точному значению измеряемой величины

В какой последовательности выполняют оценку точности результатов равноточных измерений?

Её выполняют в следующей последовательности:

- вычисляют значение арифметической средины X (среднего арифметического);

- вычисляют значение средней квадратической ошибки(ср. кв.ош.) m отдельного измерения;

- вычисляют значение ср.кв.ош. М арифметической средины.

Что понимают под арифметической срединой? Каким образом её определяют по результатам измерений?

Если в результате равноточных измерений получен ряд измеренных величин l ₁, l ₂, l ₃ ... l _{n ,} а X - точноезначение измеряемой величины, то можно написать ряд случайных ошибок: 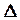₁ = l ₁ - X; 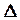₂ = l ₂ - X... 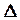_n= = l _n - X /

Образовав сумму этих ошибок 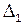+ 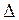₂ + 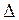₃ +...+ 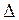_n = l₁ + l₂ + + l₃ +...+ l _n , получим [ 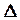] = [ l ] - nХ.

Разделив обе части последнего соотношения на n, имеем

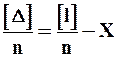. (6)

Согласно свойству случайных ошибок 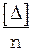при 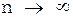стремится к нулю. Поэтому 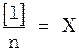, то-есть .

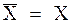Следовательно, среднее арифметическое 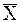из l измерений выражается формулой

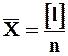. (7)

Кроме того, среднее арифметическое из l измерений стремится к истинному значению измеряемой величины при большом числе измерений n.