В) Оценка точности измерений по формуле Ф. Бесселя ( по вероятнейшим уклонениям )

При выполнении измерений истинное значение измеряемой величины, как правило, неизвестно. В этом случае ср.кв.ош. отдельного измерения вычисляют по вероятнейшим уклонениям V измеренных величин от их среднего арифметического.

Формулу для оценки результатов измерений по вероятнейшим уклонениям вывел немецкий астроном Ф. Бессель, которая представляется в виде

m = 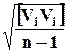= 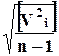, (10)

где V_i - уклонение отдельных измерений l _i от их среднего арифметического l _ср (V_i = l _i - l _ср );

n - число измерений.

Среднюю квадратическую ошибку М среднего результата измерения

в этом случае вычисляют по формуле

М = 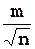. (11)

Пример обработки результатов измерения длины линии приводится в таблице 2.

Таблица 2 Обработка результатов измерений по формуле Ф. Бесселя

№ № Измеренная

измерений величина, V_i, см V² _i,см

l _i, м

1 125.10 0 0

2 125.12 + 2 4

3 125.08 - 2 4

4 125.08 - 2 4

5 125.12 + 2 4

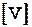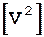n = 5 l ср = 125.10 м =0 =16

m = 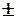2 см, М = 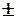0.9 см.