Чтобы выполнить оценку точности измерений, необходимо оценить прежде всего точность отдельного измерения. Казалось бы естественным взять для этого среднее арифметическое из всех случайных ошибок. Однако при этом на величину средней ошибки влияли бы разные знаки отдельных ошибок и может случиться так, что ряд с крупными отдельными ошибками получил бы меньшую среднюю ошибку, чем ряд с меньшими ошибками.
Если взять среднее арифметическое из абсолютных значений случайных ошибок, то при этом не будет достаточно отражено наличие в данном ряде отдельных сравнительно крупных ошибок.
При выборе критерия для оценки точности ряда измерений необходимо иметь в виду, что результат должен быть одинаково ошибочным, будет ли он больше или меньше истинного значения измеряемой величины. Кроме того, чем крупнее в данном ряде отдельные ошибки, тем меньше должна быть его точность.
Этим условиям лучше всего удовлетворяет средняя квадратическая ошибка результата измерения, выражаемая соотношением
m = 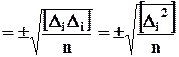 , (8)
, (8)
где 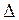 i - разности измеренных величин l i и истинных значений X
i - разности измеренных величин l i и истинных значений X
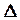 i = l i - X, (9)
i = l i - X, (9)
известнымкак формула К. Гаусса
Пример обработки результатов измерения длины линии представлен в таблице 1.
Таблица 1 Обработка результатов измерения длины линии по формуле К. Гаусса
 |
№№ Измеренная Истинная Ошибки
измере- длинадлина 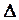 i, см
i, см 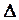 i2,см
i2,см
ний l i ,м X, м
1 110.01 110.01 0 0
2 03 + 2 4
3 02 +1 1
4 05 +4 16
5 04 +3 9
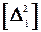 = 30
= 30
m = 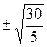 =
= 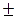 2.45 см.
2.45 см.
Утроенное значение ср.кв.ош. принимается в качестве предельной ошибки D пр = 3m при вероятности р = 0.997. При вероятности р = 0.99 предельная ошибка D пр = 2.5 m, а при вероятности р = 0.95 D пр. = 2 m
 2015-04-17
2015-04-17 1738
1738
