Математическая лингвистика и семиотика - самые «молодые» методы формализованного отображения систем. Включение их в разряд математических нельзя считать общепризнанным.
Некоторые исследователи (например, Ю.А. Шрендер) считают, что лингвистика в силу специфических особенностей, позволяющих моделировать развивающиеся системы и процессы (что обеспечивается отсутствием закона исключенного третьего), не является математикой в сложившемся понимании этого термина. В то же время французская школа математиков считает математическую лингвистику разделом современной математики.
Математическая лингвистика возникла во второй половине прошлого столетия как средство формализованного изучения естественных языков и вначале развивалась как алгебраическая лингвистика. Первые полезные результаты алгебраической лингвистики связаны со структуралистским (дескриптивным) подходом. Однако в силу отсутствия в тот период концепции развития языка эти работы привели к еще большему тупику в по пытках пос троения универсал ьной грамматики, и был период, когда структурализм считался неперспективным направлением развития науки о языке и даже был гоним.
Активное возрождение математической лингвистики началось в 50-60-е гг. XX века и связано в значительной степени с потребностями прикладных технических дисциплин, усложнившиеся задачи которых перестали удовлетворять методы классической математики, а в ряде случаев - и формальной математической логики.
В период уменьшения интереса к математической лингвистике появилось статистическое направление, которое называют статистической лингвистикой или лингвистической статистикой.
Семиотика возникла как наука о знаках, знаковых системах. Однако некоторые школы, развивающие семиотические представления, настолько равноправно пользуются в семиотике понятиями математической лингвистики, такими, как тезаурус, грамматика, семантика и т. п. (характеризуемыми ниже), не выделяя при этом в отдельное направление лингвосемиотику (как это делает, например, Ю.С. Степанов, что часто трудно определить, к какой области относится модель - математической лингвистике или семиотике.
В то же время именно в лингвосемиотике достигнуты наиболее конструктивные результаты, которые могут быть полезны при исследовании систем различной физической природы, а другие применения семиотики как науки о знаках носят в большей мере характер методологического средства для поясн ения р езультатов, которые ранее были получены в геометрии, алгебре и других разделах математики.
Поэтому мы решили для целей приложения математической лингвистики, и семиотики к системным исследованиям рассматривать эти направления совместно, не оговаривая особо, что фактически речь пойдет о лингвосемиотике.
Основными понятиями, на которых базируются лингвистические представления, являются понятия: тезаурус, грамматика, семантика, прагматика.
Термин тезаурус (от греч. "thesauros" - сокровищница, богатство, клад, запас и т. п.) в общем случае характеризует «совокупность научных знаний о явлениях и законах внешнего мира и духовной деятельности людей, накопленную всем человеческим обществом». Этот термин был введен в современную литера туру по языкознанию и информатике в 1956 году Кембриджской группой по изучению языков. В то же время термин существовал раньше: в эпоху Возрождения тезаурусами называли энциклопедии. В математической лингвистике и семиотике термин тезаурус используется в более узком смысле, для характеристики конкретного языка, его многоуровневой структуры. Для этих целей удобно пользоваться одним из принятых в лингвистике определений тезауруса как «множества смысловырожающих элементов языка с заданными смысловыми отношениями».
Это определение позволяет представить структуру языка в виде уровней (страт) множеств (например, слов, словосочетаний, предложений, абзацев и т. п.), смысловыражающие элементы каждого из которых формируются из смысловыражающих элементов предшествующих структурных уровней (см. рис. 2,11).
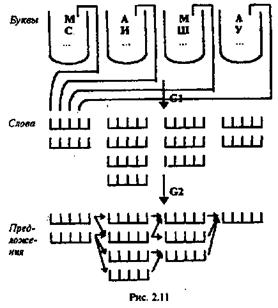
Правила (G1, G2) формирования смысловыражающих элементов второго и третьего уровней в тезаурус не входят, в тезаурусе определяется только вид и наименование уровня, характер и вид смысловыражающих элементов.
Иногда вместо термина смысловыражающие элементы используется термин синтаксические единицы тезауруса. На наш взгляд, это менее удачный термин, так как при формировании элементов нового множества смысловыражающих элементов каждого последующего уровня (при образовании слов из букв, фраз и предложений из слов) у элементов вновь образованного множества по является новый смысл, т. е. как бы проявляется закономерность целостности, и это хорошо отражает термин "смысловыражающий элемент".
В таком толковании понятие тезауруса можно конструктивно использовать при создании искусственных языков - языков моделирования, автоматизации проектирования, информационно-поисковых языков. Оно позволяет охарактеризовать язык с точки зрения уровней обобщения, ввести правила их использования при индексировании информации.
Можно говорить о глубине тезауруса того или иного языка, характеризуемой числом уровней, о видах уровней обобщения, и, пользуясь этими понятиями, сравнивать языки, выбирать более подходящий для рассматриваемой задачи или, охарактеризовав структуру языка, организовать процесс его разработки.
Под гра мматикой (которую иногда называют синтактикой, синтаксисом, что сужает понятие грамматики, исключая из него морфологию) понимаются правила, с помощью которых формируются смысловыражающие элементы языка (на рис. 2.11 два вида правил - G1 и G2, которые иногда называют грамматиками 1-го и 2-го рода). Пользуясь этими правилами, можно «порождать» (формировать) грамматически (синтаксически) правильные конструкции или распознавать их грамматическую правильность.
Термин грамматика употребляется в лингвистике и как укороченная замена термина "формальная грамматика", который имеет иной смысл и будет охарактеризован ниже.
Под семантикой понимается со держание, значение, смысл формируемых или распознаваемых конструкция языка; под прагматикой - полезность для данной цели, задачи.
В естественном языке различить понятия, с помощью которых характеризуются термины семантика и прагматика, трудно; обычно пояснить различие можно лишь при парном сопоставлении терминов:
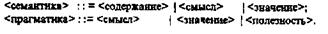
Поэтому принято рассматривать эти понятия на примерах. Поясним различие между семантически и прагматически правильными конструкциями языка на следующих легко запоминающихся примерах.
Традиционно для пояснения синтаксической правильности и семантической бессмыслицы используется предложенный Л.В. Щербой пример «Г локая куздра тщето борзданула бокра и курдычет бокрёнка» (в котором просто нет ни одного слова естественного языка, имеющего смысл). Но примеры можно найти и в естественной речи.
Предложение "Муха лукаво всплеснула зубами" синтаксически правильное, но не имеет смысла в естественном русском языке в обиходном, широком употреблении.
т. е. является с точки зрения пользователей русским языком семантически неправильным (исключим пока гипотетическую ситуацию сказки, в которой муха может быть наделена указанными свойствами).
Другое предложение "Маленькая девочка собирает цветы на лугу" - синтаксически и семантически правильное. Однако для директора завода (если это луг, а не заводской газон, и - учтем личный фактор - если эта девочка не его дочь) это предложение не несет никакой информации, т. е. прагматически (с точки зрения целей руководителя) является неправильным. Другое дело, если "Иванов (который в данный момент должен находиться на рабочем месте) собирает цветы на лугу". Тогда это предложение было бы и прагматически правильным.
Возвратимся теперь к примеру с мухой. Приведенное предложение, семантически неправильное, может в гипотетической ситуации сказки оказаться прагматически правильным, что важно иметь в виду при применении лингвистических представлений.
При создании и использовании искусственных языков применяют такие понятия структурной лингвистики, как порождающая и распознающая грамматика.
Под порождающей грамматикой понимается совокупность правил, с помощью которых обеспечивается возможность формирования (порождения) из первичных элементов (словаря) синтаксически правильных конструкций. Под распознающей грамматикой - правила, с помощью которых обеспечивается возможность распознавания синтаксической правильности предложений, фраз или других фрагментов языка.
Все рассмотренные понятия в равной мере используются как в математической лингвистике, так и в лингвистической семиотике. Некоторую условную границу между ними можно провести, лишь введя понятие классы формальных грамматик (как теорий математической лингвистики).
На базе лингвистических представлений развивается теория формальных грамматик Н.Хомского. Классы формальных грамматик Н.Хомского считаются основой теории формальных языков.
Формальный язык определяют как множество (конечное или бес конечное) предложений (или " цепочек"), каждое из которых имеет конечную длину и построено с помощью некоторых операций (правил) из конечного множества элементов (символов), составляющих алфа вит языка.
Формальную грамматику определяют в виде четверки множеств:
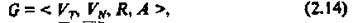
где VT - множество основных или терминальных символов; VN -множество вспомогательных или нетерминальных символов; R -множество правил вывода, или продукций, которые могут иметь вид:

т. е. (β - цепочка конечной длины из терминальных и нетерминальных символов множеств VТ и VN,
а
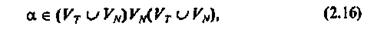
т. е. α является цепочкой из терминальных и нетерминальных сим волов, содержащей по крайней мере один нетерминальный символ из VN;
А - множество аксиом (в грамматиках комбинаторного типа, к которым относятся грамматики Н. Хомского, А состоит из одного начального символа S, причем S 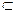 VN.
VN.
Учитывая, что в литературе по формальным грамматикам, как правило, не стремятся к содержательной интерпретации получаемых выводов, а рассматривают лишь формальную сторону процессов порождения и распознавание принадлежности цепочек к соответствующему классу грамматик, приведем содержательный пример порождающей грамматики.
Предположим, дано:

Применяя правила R левой части (2.17) в приведенной последовательности, получим:
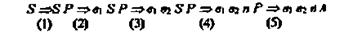
Это - формальная сторона процесса порождения. Для того, чтобы получить интерпретируемое выражение, нужно расшифровать терминальные символы, включенные в VN, где в1 -«все», в2 –«возрасты», п -«покорны», л-« любви».
Тогда полученное предложение «в1в2пл» - «все возрасты покорны любви».
Если изменить последовательность применения правил, то будут получаться другие предложения. Например, еслиприменить правила в последовательности (1) 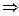 (3)
(3) 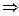 (2)
(2) 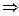 (4)
(4) 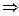 (5), то получится «возрасты все покорны любви». Если применить не все правила: например, (1)
(5), то получится «возрасты все покорны любви». Если применить не все правила: например, (1) 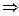 (2)
(2) 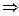 (4)
(4) 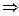 (5), то получим «все покорны любви».
(5), то получим «все покорны любви».
Если же попытаться получить предложение, как у А.С. Пушкина – «Любви все возрасты покорны», то, как бы мы не меняли последовательность правил, получить эту фразу не удается. Нужно изменить первое правило: вместо S→SP включить в R правило S→ PS.
Из примера видно, что вид порождаемых цепочек (предложений) зависит от вида правил (исчисления) и от последовательности их применения (алгоритма).
С помощью приведенного примера легко также продемонстрировать тесную связь понятия «грамматически правильный» с языком (грамматикой).
Распознающая грамматика для рассматриваемого примера будет содержать как бы "перевернутые" правила - правая часть (2.17), которые должны применяться в обратной последовательности. Пример представления анализа правильности пред ложения с помощью правил распознающей грамматики приведен на рис. 2.12.
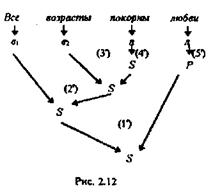
При распознавании правильности предложения если не оговаривать, что предложение (цепочка) грамматически правильно с точки зрения правил данного формального языка, то можно. пользуясь формальной грамматикой в первоначальном виде, получить вывод, что приведенная фраза Пушкина грамматически неправильна с точки зрения правил грамматики (2.18).
Действительно, с точки зрения правил грамматики для построения делового текста, которым соответствуют правила (2.18), другие поэтические строки часто получали бы формальную оценку "грамматически неправильно". И, напротив, еcли бы мы построили грамматику на основе анализа пушкинского стиля, то в деловом тексте получили бы предложения типа "Я решение свое принял правильное" (подобно фразе "Я памятник себе воздвиг нерукотворный").
Сказанное позволяет легко представить полезность определения формальной грамматики при создании языка моделирования соответствующего литературного или музыкального произведения - пародий, подражательств или, как иногда принято говорить, произведений соответствующего стиля или класса (например, известны работы Р.Х. Зарипова по моделированию музыкальных произведений в стиле, или в классе, массовых советских песен, моделирование процесса сочинения стихотворных произведений и т. п.).
Подобным же образом можно моделировать порождение деловых писем или других документов, имеющих, как правило, не только формализованный стиль, но и формальную структуру.
Аналогично можно создавать языки моделирования структур, языки автоматизации проектирования сложных устройств и систем определенного вида (класса).
Основу подобных работ составляют идеи, которые можно пояс нить с помощью классов грамматик, впервые предложенных Н.Хомским.
Разделение грамматик на классы определяется видом правил вы вода R. В зависимости от правил R можно выделить четыре основных, наиболее часто рассматриваемых класса грамматик (в полной теории формальных грамматик с правилами типа подстановки есть и промежуточные классы):
1-й класс. На правила вывода накладывается только одно требование, чтобы в левой части правила вывода было всегда меньше символов, чем в правой, т. е. чтобы правила были неукорачивающими, не уменьшали число символов в выводимых цепочках. Этот класс грамматик обычно так и называют неукорачивающими (НУ- грамматиками). Иногда их также называют грамматиками типа ноль (нулевого типа) или алгоритмическими.
2-й класс. На правила вывода, помимо требований неукорачиваемости, наклады вается ограничение, чтобы на каждом шаге изменялся только один символ в кон тексте. т. е. чтобы ZI B Z2→Z1 W Z2, где В - один нетерминальный символ, W -непустая цепочка символов, т. е. W≠ 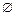 . Грамматику такого вида называют контекстной, контекстно-связанной или иногда применяют термин - грамматика непосредственных составляющих (НС-грамматики).
. Грамматику такого вида называют контекстной, контекстно-связанной или иногда применяют термин - грамматика непосредственных составляющих (НС-грамматики).
3-й класс. Если, кроме неукорачиваемости требуется, чтобы правила имели вид В→β (т. е. а всегда состоит из одного вспомогательного символа), то грамматику такого типа называют бесконтекстной или контекстно-свободной (КС-грамматика).
4-й класс. Ес ли на правила вывода накладывается по сравнению с третьим классом еще одно ограничение, требующее, чтобы в правилах вывода нетерминальный символ всегда стоял справа или слева, т. е. с одной стороны, то грамматику называют автоматной (А-грамматикой). Если нетерминальный символ стоит слева, т. е. правила имеют вид А→ a В или A →a, где (A, В) 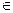 VN, a
VN, a 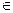 VT, автоматная грамматика является праволинейной, если нетерминальный символ стоит справа - то автоматную грамматику называют леволинейной.
VT, автоматная грамматика является праволинейной, если нетерминальный символ стоит справа - то автоматную грамматику называют леволинейной.
В теории формальных грамматик показывается, что имеет место следующее соотношение:
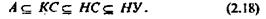
Иногда доказывают, что имеет место строгое вхождение:
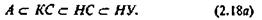
При исследовании разных классов формальных грамматик по лучены результаты, которые позволяют сделать вывод, что по мере уменьшения числа ограничений, накладываемых на правила вы вода, т. е. по мере продвижения в (2.18) слева направо, в языке увеличивается возможность отображение смысла (повышается смысловыражающая способность языка, т. е. возможность выражения с помощью формальных правил семантических особенностей проблемной ситуации): говорят, что формальная система становится более богатой. Однако при этом в языке растет число алгоритмически неразрешимых проблем, т. е. увеличивается число положений, истинность или ложность которых не может быть доказана в рамках формальной системы языка.
Здесь мы сталкиваемся фактически с гёделевской проблемой, которая в теории формальных языков обсуждается обычно в терминах этой теории. А именно: вводится понятие «операция определена (или не определена) на множестве языков данного класса»; и считают, что операция определена на множестве языков данного класса, если после применения ее к языкам, входящим в это множество, получается язык, принадлежащий множеству языков этого
класса. Например, если Я1 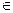 КС и Я2
КС и Я2 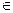 КС, и если (Я1
КС, и если (Я1 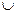 Я2)
Я2) 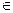 КС, то операция объединения
КС, то операция объединения 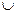 определена на классе КС-языков.
определена на классе КС-языков.
Характеризуя с помощью введенного понятия классы языков, отмечают, что в последовательности (2.18) по мере продвижения слева направо увеличивается число операций, которые не определены на множестве языков данного класса.
Здесь, правда, следует оговорить, что дело обстоит не так прямолинейно. Точнее было бы сказать, что для большого числа операций нет доказательств, что они определены на классах НС-языков и НУ-языков, т. с. эти доказательства становятся сложнее или вообще (в силу теоремы Гёделя) нереалнзуемы средствами теории формальных грамматик.
В упрощенном виде мы представили проблему для того, чтобы обратить внимание тех, кто будет заниматься разработкой языков программирования или программных систем, языков моделирования, автоматизации проектирования, на необходимость учитывать закономерность: чем большими смысловыражающими возможностями обладает знаковая система, тем в большей мере растет в ней число алгоритмически неразрешимых проблем (т. е. тем менее доказательны в ней формальные процедуры).
При выходе в класс произвольных грамматик, в котором не выполняется даже условие неукорачиваемости, доказать допустимость тех или иных формальных пре образований средствами математической лингвистики практически невозможно, и поэтому в поисках новых средств исследователи обратились к семиотическим представлениям. Здесь можно провести как бы формальную границу между лингвистикой и семиотикой.
Семиотические представления пользуются другими по сравнению с математической лингвистикой средствами исследования семантических возможностей языков. В частности, понятием треугольника Фреге [2.27, 2.62 и др.], согласно которому любой знак имеет форму: синтаксис (означаемое знака) и семантику (смысл, значение).
Такая исходная терминология позволяет отойти от представлений формальных грамматик Н.Хомского, имеющих отношения типа подстановки, и конструировать грамматику, используя более широкий спектр отношений.
В частности, на границе лингвистики и семиотики возникли языки синтагматического типа, т. е. языки, использующие правила типа {аi rk bj), называемые синтагмой, где аi 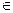 A, bj
A, bj 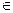 В - взаимодействующие множества (подклассы) исходных понятий языка; rk
В - взаимодействующие множества (подклассы) исходных понятий языка; rk 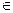 R - множество отношений, которые могут иметь произвольный вид. Однако такая свобода, как уже отмечалось выше, приводит к увеличению числа антиномий в языке.
R - множество отношений, которые могут иметь произвольный вид. Однако такая свобода, как уже отмечалось выше, приводит к увеличению числа антиномий в языке.
Например, для информационно-поискового языка это означает ухудшение его качеств (в частности - релевантности, т. е. соответствия выдачи запросу пользователя) в силу того, что при реализации поискового алгоритма могут возникнуть замкнутые циклы, обусловленные противоречивыми правилами грамматики языка.
 Поэтому используемые отношения все же пытаются конкретизировать.
Поэтому используемые отношения все же пытаются конкретизировать.
В частности, Ю.А. Шрейдер [2.61] исследовал возможности использования отношений эквивалентности, толерантности и строгого порядка, определяемых на основе свойств рефлексивности, симметричности и транзитивности (табл. 2.9).
С примерами применения этих отношений для отображения фраз и текстов естественного языка можно познакомиться в (2.61, 2.62]. Но для пояснения возможностей, появляющихся при таком подходе к созданию языка проиллюстрируем применение отношения толерантности.
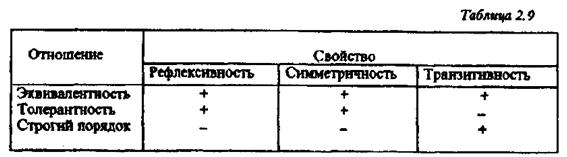
Как видно из таблицы, по определению толерантность - особый вид сходства, при котором сопоставляемые элементы языка находятся в отношении, обладающем рефлексивностью и симметричностью, но не обладающем транзитивностью. Это означает, что, например, если при сопоставлении слов ввести допустимую ошибку в один символ, то отношение сходства между первым и вторым словами могут быть признаны (с точностью до допусти мой ошибки) рефлексивным и симметричным; аналогично - между вторым и третьим; но первое и третье слова уже могут отличаться не одним, а двумя символами, и сходство между ними можно вообще не обнаружить, т. е. не будет выполнено отношение транзитивности.
В [2.61] приводится образный пример, как в результате приметши такого от ношения можно получить из "мухи" "слона" (г. е. из слова "муха" получить слово "слон", а также иллюстрация понятия транзитивности с помощью гравюры голландского художника М.К.Эсхера "Небо и вода" (на которой едва различимые пре образования на каждом шаге сверху вниз постепенно превращают контуры птиц в контуры рыб).
Возникновение подобных ситуаций важно учитывать при раз работке языков для формального кодирования передачи текстов и восстановления их в месте приема.
С помощью отношения толерантности можно отобразить некоторые отношения между словами естественного языка.
Например:

где τ - операция установления сходства.
Приведенные соотношения (2.19) означают, что в синтагме "рама τ стол" имеет место отношение сходства с точностью до рефлексии и симметрии, в синтагме "стол τ книгу" - тоже, а между элементами синтагмы прам-а" - "книг-у" сходства нет в силу невыполнения по определению для рассматриваемого отношения свойства транзитивности.
Попытаемся интерпретировать формальную запись (2.19). Содержательный анализ этих соотношений позволяет понять, что в них отражено сходство по падежу: слова мужского рода ("стол") могут употребляться в русском языке в одинаковой форме в именительном (первая строка) и винительном (вторая строка) падеже, в то время, как слова женского рода имеют в этих падежах разную форму, что и обусловило нетранзитивность.
Аналогично можно отобразить сходство по роду, так как в русском языке могут использоваться одни и те же имена для женщин и мужчин, что в тексте без дополни тельных пояснений или учета формы глагола может оказаться нераспознаваемым. Можно также отразить понятие места в предложения или места предложения в абзаце и т. п.
Таким образом, вводя в язык отношение толерантности (напри мер. путем формирования классов толерантности) можно отразить в языке взаимоотношения между словами и высказываниями более полно и точно, чем это позволяют делать отношения математической логики или грамматик Н.Хомского. Такие языки необходимы при расшифровке древних рукописей, при автоматизации процесса перевода с одного языка на другой.
Однако, следует иметь в виду, что создание подобных языков - весьма сложный и трудоемкий процесс, и поэтому в практике информационного поиска или разработки языков моделирования в тех случаях, когда есть возможность отразить особенности моделируемой ситуации иным способом, рассматриваемый подход не применяют.
В частности, при разработке некоторых информационно-поисковых языков было предложено вводить при индексировании текста понятия "указатели роли", "указатели связи", которые легче интерпретируются при ручном индексировании, чем понятие толерантности. В то же время при автоматизации индексирования может воз никнуть необходимость в использовании отношений, приведенных в табл. 2.9, поскольку они. обладая большими но сравнению с лингвистическими представления ми смысловыражаюшнмн возможностями, все же базируются на определенной формальной основе, которая может позволить сделать язык более алгоритмизируемым.
 2015-04-17
2015-04-17 1334
1334








