Логические методы

Базовыми понятиями математической логики являются высказывание, предикат, логические функции (операции) кванторы, логический базис, логические законы (законы алгебры логики).

Под высказыванием в алгебре логики понимается повествовательное предложение (суждение), которое характеризуется определенным значением истинности.

В простейших случаях используется два значения истинности: "истинно" - "ложно", "да" - "нет", "1" - "0". Такая алгебра логики, в которой переменная может принимать только два значения истинности, называется бинарной алгеброй логики Буля (по имени создателя алгебры логики).

Предикат - выражение, грамматически имеющее форму высказывания, но содержащее переменные некоторых подмножеств, на которых они определены.

При замене переменных элементами соответствующего подмножества предикат обращается в высказывание. Обычно переменная стоит в предикативной части предложения, лежащего в основе высказывания (например, «быть Х -вым карандашом», где X может принимать значения «красным», «синим» и т. д.), но в принципе это не обязательно (и возможны предикаты "X - река", где X -"Волга", "Днепр" и т.д.).

Частным случаем предиката является пропозиционная функция - функция одной или нескольких переменных, принимающих значения в множестве, состоящем из двух элементов «1» - «0».

Применение переменных высказываний служит для выражения общности и позволяет формулировать законы алгебры логики для любых высказываний данного вида.

Из одного или нескольких высказываний или предикатов можно образовать новые высказывания или предикаты. Объединение простых высказываний в сложные производится без учета смысла этих высказываний (предикатов) на основе определенных логических правил (операций, функций).

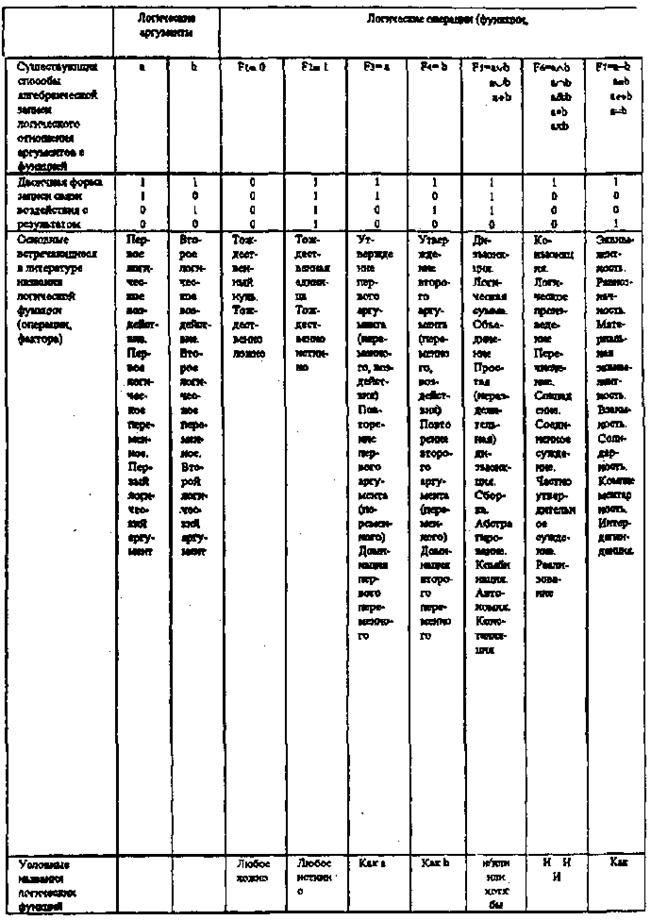
Число простейших логических функций в конкретной алгебре логики зависит от количества значений истинности n:

Для двузначной булевой алгебры логики N определяется числом возможных двоичных наборов (n =2): N =16. При n =3 можно образовать N=256 логических функций.

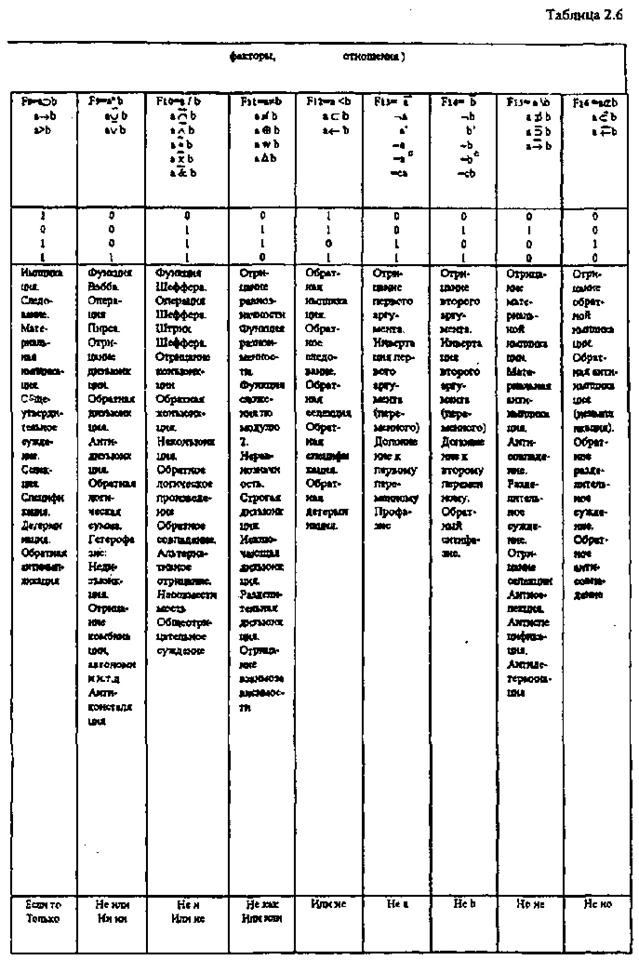
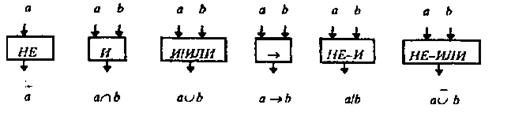
Функции бинарной алгебры логики приведены в табл. 2.6, в которой собраны формы записи и наименования функций, встречающиеся в различных литературных источниках.

Кроме логических функций, в логике предикатов имеются еще операции квантификации - кванторы. Это специальные операции, которые служат для выражения общности суждений и связанных с ними понятий (табл. 2.7) и позволяют на формальном языке исчисления предикатов говорить не об одном объекте, а о целом классе объектов.

Полную систему логических функций называют логическим базисом. Для того, чтобы система функций представляла собой базис. она должна обладать определенными свойствами.

В частности, чтобы система функций была полной, необходимо и достаточно. чтобы она содержала хотя бы одну функцию: не сохраняющую константу единица, не сохраняющую константу ноль, нелинейную, немонотонную, несамодвойственную.

Полный логический базис содержит избыточное число функций. Такая система функций может остаться базисом при удалении из нее некоторых функций. Удаление функций можно производить до тех пор, пока система не станет такой, что удалении из нее хотя бы одной из функций, ее образующих, будет приводить к невыполнению перечисленных требований к базису. Такую систему называют минимальным базисом.

Минимальными базисами бинарной алгебры логики являются базисы, включающие только две функции {, 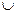} {, }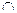. Функция отрицания не сохраняет константы ноль и единицу и не является монотонной, функции дизъюнкции 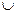и конъюнкции 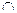обеспечивают нелинейность не являются самодвойственными (в силу приведенных в табл. 2.8 теорем де-Моргана),

В этой связи существуют понятия дизъюнктивно-нормальной и конъюнктивно-нормальной формы, всегда удовлетворяющие требованиям базиса.

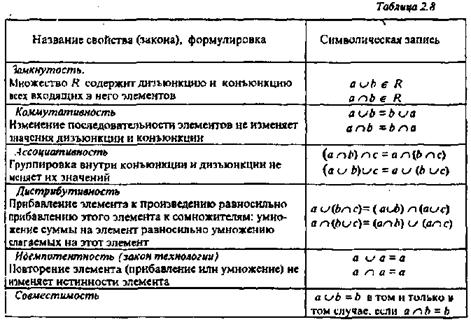
В условиях выполнения требований к базису в алгебре логики доказывают теоремы, демонстрирующие свойства операций над высказываниями. Применяя эти теоремы, формально можно получить правильный результат, не вникая в смысл проводимых исследований. Примеры этих теорем или логических законов приведены в табл. 2.8.

Из элементарных функций алгебры логики формируют последовательности действий, отображающие процессы в системе от входа до выхода, т. е. логические алгоритмы.

На рис. 2.7 и 2.8 проиллюстрирована разная запись одного и то го же алгоритма (соответствие обозначений рис. 2.7 и 2.8 приведено на рис. 2.9).

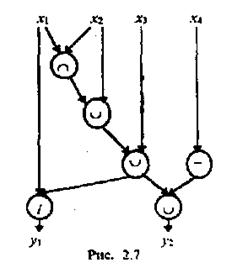
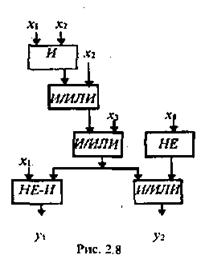
Этот же алгоритм может быть записан следующим образом:

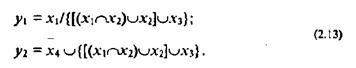
Существует много форм записи логических алгоритмов: в виде функций алгебры логики (2.13), в форме таблиц или матриц, «машин Тьюринга», логических схем по А.А.Ляпунову, с помощью рекурсивных функций, на языке нормальных алгоритмов А.А. Маркова, в виде программ для вычислительных машин на одном из языков программирования, в форме диаграмм Насси-Шнайдермана. С основными способами представления алгоритмов можно по знакомиться в [2.27, 2.39, 2.65 и др.].

Логические алгоритмы могут преобразовываться с использованием логических законов. Пример применения одного из законов (теоремы А. де-Моргана) приведен на рис. 2.10.

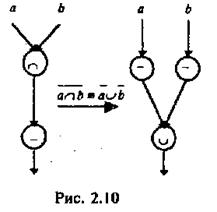
На базе логических представлений возникли и развиваются теории логического анализа и логического синтеза. Эти теории основаны на применении средств алгебры логики к задачам анализа и синтеза структур исследуемых систем, а также к задачам принятия решений в сложных проблемных ситуациях, возникающих в системах или при взаимодействии систем.

Задача логического анализа состоит в описании поведения системы с известной структурой набором системно-логических уравнений (функций алгебры логики - ФАЛ) и исследования полученного логического выражения с целью его минимизации, т.е. выяснения, нельзя ли получить более простую структуру (схему), содержащую меньшее число элементов (состояний), но осуществляющую требуемые преобразования. Такие задачи возникают, например, при создании автоматических систем контроля неисправностей, систем автоматического резервирования, обеспечения надежности и т.д.

Задача логического синтеза заключается в том, чтобы по известному поведению системы определить ее структуру (в случаях, если она неизвестна или не полностью известна), т. е. сопоставить системе некоторый "автомат" - "черный ящик" с известными входными и выходными воздействиями.

Таким образом, при логическом анализе задача сводится к минимизации ФАЛ, т. е. к оптимизации в некотором смысле логического алгоритма. Задача логического синтеза сложнее, она обычно решается путем последовательных приближений, и на промежуточных этапах здесь также может быть полезна минимизация ФАЛ.

Минимизация осуществляется путем применения законов алгебры логики, приведенных в табл. 2.8. Наиболее известными методами минимизации ФА Л являются: метод минимизирующих карт или таблиц (конъюнктивных или дизъюнктивных, импликатных); метод неопределенных коэффициентов; геометрические методы, метод Блека-Порецкого (с обзором методов минимизации ФАЛ можно познакомиться в [2.39], где даны ссылки на соответствующие первоисточники).

При возрастании числа переменных для минимизации ФАЛ применяют ЭВМ. При этом логический алгоритм нужно перевести на один из языков программирования, или при логическом анализе сложных ситуаций - разрабатывают промежуточные языки проектирования или моделирования процессов управления (например, язык БИТ Э.Ф. Скороходъко, логический язык представления алгоритмов синтеза ЛЯПАС А.Д. Закревского и др.).

Специфические особенности задачи логического синтеза при описании системы логическим автоматом вызвали возникновение и развитие самостоятельной научной дисциплины - теории автома тов.

Логические методы представления систем возникли как детерминистские, но в дальнейшем стали предприниматься попытки их расширения в сторону вероятностных оценок.

Логические представления сыграли большую роль в развитии теоретической основы алгоритмизации и программирования. В частности, они лежат в основе теории алгорифмов (в дальнейшей -алгоритмов) А.А. Маркова.

Логические представления применяют в случаях исследований новых структур систем разной природы (технических объектов, текстов и др.), в которых характер в заимодействи я между элемен тами еще не настолько ясен, чтобы возможно было их представление аналитическими методами, а статистические исследования либо затруднены, либо не привели к выявлению устойчивых закономерностей.

В то же время следует иметь в виду, что с помощью логических алгоритмов можно описывать не любые отношения, а лишь те, которые предусмотрены законами алгебры логики.

В настоящее время логические представления широко применяются при исследовании и разработке автоматов разного рода, автоматических систем контроля, при решении задач распознавания образов. На их основе развивается самостоятельный раздел теории формальных языков моделирования проблемных ситуаций и текстов.

В то же время смысловыражающие возможности логических методов ограничены базисом и не всегда позволяют адекватно отобразить реальную проблемную ситуацию. Поэтому стали пред приниматься попытки создания вначале тернарной логики, а затем - и логик, в которых переменная может принимать не только крайние значения «истинно» - «ложно», но и какие-либо из промежуточных - многозначных логик, вплоть до непрерывной.

Однако отметим, что даже для тернарной логики В.Т. Кулику так и не уда лось создать непротиворечивый логический базис, и он обратился к созданию информационных языков моделирования на основе лингвистических представлений. Неудача попыток создания многозначных логик объяснима, если учесть, что вся математика, в т. ч. математическая логика для того, чтобы соответствовать принципам строго формальной дедуктивной системы (с учетом, конечно, теоремы Геделя), базируется на законе исключенного третьего ( г. е. на предположении, что всякое событие, положение может быть истинным или ложным, третьего не дано).

Реальная же действительность не подчиняется этому закону, и поэтому для ее моделирования необходимо либо создание подходов, основанных на формализации диалектической логики (специальное направление информационного моделирования, развивающееся на этой основе, рассматривается в гл. 3), либо использование лингвистических и семиотических представлений, которые свободны от требования выполнения закона исключенного третьего, что и является иногда основанием для того, чтобы не включать эти направления в математику.