Пример 1. Найти угол между диагоналями параллелограмма, построенного на векторах 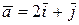 и
и 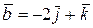 .
.
Решение. Диагоналями параллелограмма являются векторы 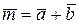 и
и 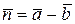 . Тогда
. Тогда 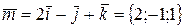 ,
, 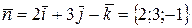 ,
, 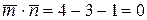 , следовательно,
, следовательно, 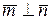 – угол между диагоналями равен
– угол между диагоналями равен 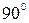 .
.
Ответ. 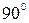 .
.
Пример 2. Дано: 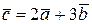 ,
, 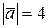 ,
, 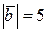 ,
, 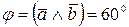 . Вычислить
. Вычислить 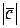 – длину вектора
– длину вектора 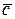 .
.
Решение. Из свойства (5) скалярного произведения 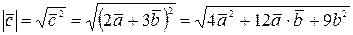 ; но
; но 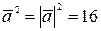 ,
, 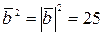 ,
, 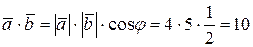 , следовательно,
, следовательно, 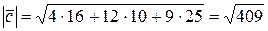 .
.
Ответ. 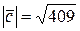 .
.
Пример 3. Упростить выражение 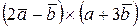 .
.
Решение. На основании свойств векторного произведения получим
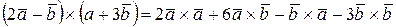 , но
, но 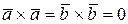 ,
, 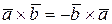 , тогда
, тогда 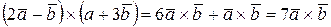 .
.
Ответ. 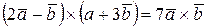 .
.
Пример 4. В треугольнике с вершинами 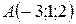 ,
, 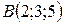 ,
, 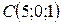 найти длину высоты
найти длину высоты 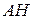 .
.
Решение. 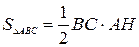 , откуда
, откуда 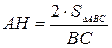 , где
, где 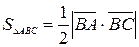 . Найдем координаты векторов:
. Найдем координаты векторов: 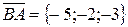 ,
, 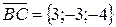 .
.
Тогда
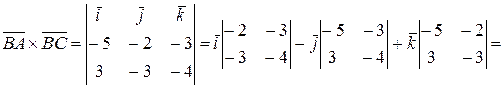
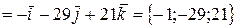 ;
;
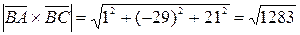 , то есть
, то есть 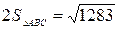 ;
;
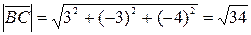 , следовательно,
, следовательно, 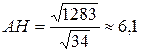 .
.
Ответ. 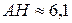
Пример 5. Доказать, что точки 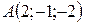 ,
, 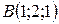 ,
, 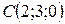 и
и 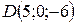 лежат в одной плоскости.
лежат в одной плоскости.
Решение. Достаточно показать, что векторы 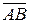 ,
, 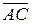 и
и 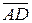 компланарны, то есть их смешанное произведение равно нулю.
компланарны, то есть их смешанное произведение равно нулю.
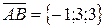 ,
, 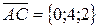 ,
, 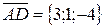 ;
;
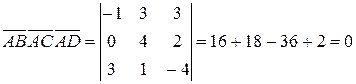
Пример 6. Найти объем тетраэдра, построенного на векторах 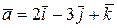 ,
, 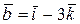 ,
, 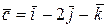 . Правой или левой является тройка векторов
. Правой или левой является тройка векторов 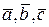 ?
?
Решение. Найдем смешанное произведение этих векторов:
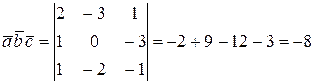 .
.
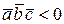 , значит, векторы образуют левую тройку;
, значит, векторы образуют левую тройку;
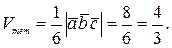
 2015-04-01
2015-04-01 19041
19041
